Overview of the undergraduate math program: Difference between revisions
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
This page describes the general structure of the the math major as well as the courses offered by our department that a major might use to complete his or her program. In general, the math major is very flexible and has very few firm requirements. THerefore all students are strongly encouraged to speak with an | This page describes the general structure of the the math major as well as the courses offered by our department that a major might use to complete his or her program. In general, the math major is very flexible and has very few firm requirements. THerefore all students are strongly encouraged to speak with an [https://www.math.wisc.edu/undergraduate/advising adviser] in order to plan and select their courses. | ||
== General Description of Math Course Levels == | == General Description of Math Course Levels == | ||
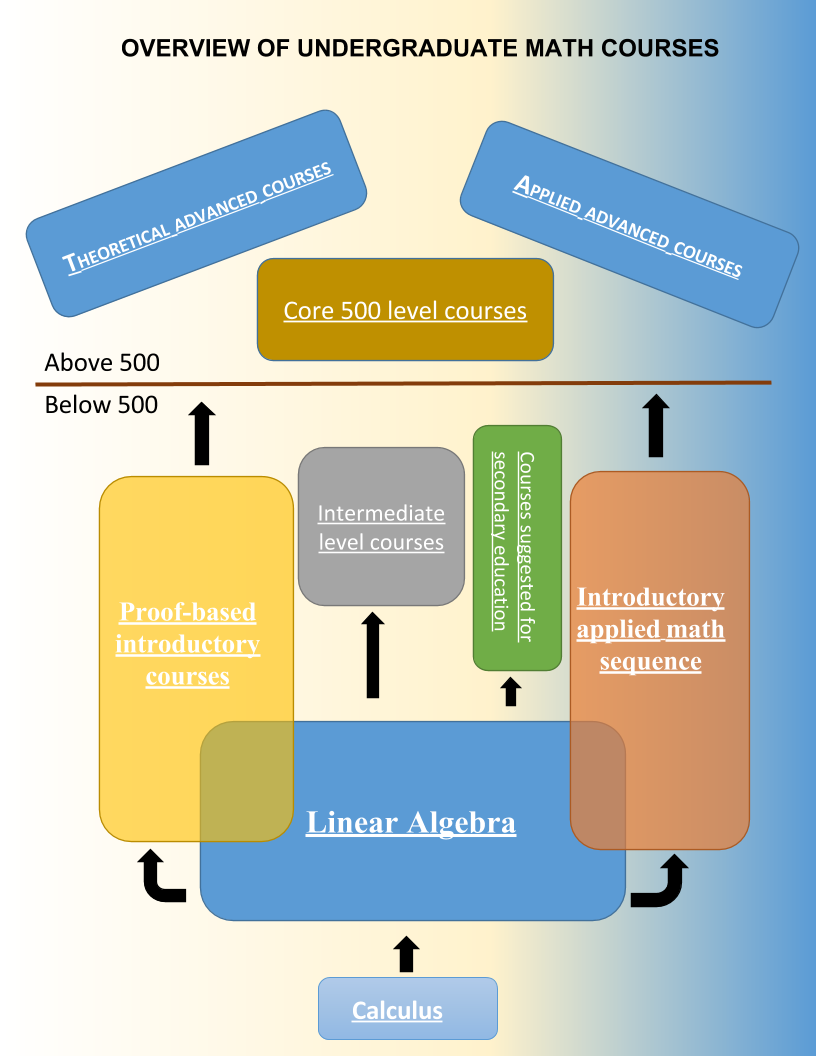
Math courses at UW-Madison are roughly grouped into three tiers: | Math courses at UW-Madison are roughly grouped into three tiers: | ||
* Classes below the 300 level are generally [[Overview_of_the_calculus_courses|calculus]] and precalculus courses or various types and flavors. Students who are interested in mathematics as a major typically complete the 221-222-234 calculus sequence (or its equivalent). Well prepared | * Classes below the 300 level are generally [[Overview_of_the_calculus_courses|calculus]] and precalculus courses or various types and flavors. Students who are interested in mathematics as a major typically complete the 221-222-234 calculus sequence (or its equivalent). Well prepared freshmen might instead consider the 375-376 honors calculus sequence as an alternative. | ||
* Classes numbered between 300 and 500 are [[Intermediate_level_undergraduate_courses|intermediate level courses]] classes. These courses typically will have some lower level prerequisites (usually Math 234) and will feature how mathematical concepts evolve into deeper theory and/or applications. At this level you will find our [[Undergraduate_Linear_Algebra_Courses|linear algebra]] courses (a major requirement) as well as courses designed specifically for students interested in [[Courses suggested for secondary education|secondary education]]. You will also find our [[Transition to proof courses]] and [[Introductory applied math sequence]]. We strongly suggest that students take courses from at least one of these two areas before moving into the advanced levels. | * Classes numbered between 300 and 500 are [[Intermediate_level_undergraduate_courses|intermediate level courses]] classes. These courses typically will have some lower level prerequisites (usually Math 234) and will feature how mathematical concepts evolve into deeper theory and/or applications. At this level you will find our [[Undergraduate_Linear_Algebra_Courses|linear algebra]] courses (a major requirement) as well as courses designed specifically for students interested in [[Courses suggested for secondary education|secondary education]]. You will also find our [[Transition to proof courses]] and [[Introductory applied math sequence]]. We strongly suggest that students take courses from at least one of these two areas before moving into the advanced levels. | ||
* Classes numbered above 500 are our [[Advanced courses|advanced courses] including the [[Core 500 level courses|core 500 level courses]] in analysis, algebra, and topology. It is our opinion that students who feel comfortable should proceed to this level as quickly as possible. In particular, those students interested in graduate study in mathematics should aim to take 4-8 courses at this level, depending on interests. | * Classes numbered above 500 are our [[Advanced courses|advanced courses]] including the [[Core 500 level courses|core 500 level courses]] in analysis, algebra, and topology. It is our opinion that students who feel comfortable should proceed to this level as quickly as possible. In particular, those students interested in graduate study in mathematics should aim to take 4-8 courses at this level, depending on interests. | ||
== Progressing Through the Math Major == | == Progressing Through the Math Major == | ||
The math major requires a course in linear algebra as well as several courses at the intermediate and advanced levels. However, most students will begin somewhere within the [[Overview_of_the_calculus_courses|calculus]] sequence. As a student near the end of the calculus sequence they should meet with an | The math major requires a course in linear algebra as well as several courses at the intermediate and advanced levels. However, most students will begin somewhere within the [[Overview_of_the_calculus_courses|calculus]] sequence. As a student near the end of the calculus sequence they should meet with an [https://www.math.wisc.edu/undergraduate/advising adviser] in order to discuss the major and associated interests. This is a good time to talk about | ||
* What [[Undergraduate_Linear_Algebra_Courses|linear algebra]] course you should take. | * What [[Undergraduate_Linear_Algebra_Courses|linear algebra]] course you should take. | ||
* If an [[Transition to proof courses|introduction to proofs]] course is a good idea. (It probably is!) | * If an [[Transition to proof courses|introduction to proofs]] course is a good idea. (It probably is!) | ||
* Are you interested in an [[Option 2 Major]]? | * Are you interested in an [[Option 2 packages|Option 2 Major]]? | ||
* What [[Advanced courses]] you should target. | * What [[Advanced courses]] you should target. | ||
Latest revision as of 21:04, 30 August 2017
This page describes the general structure of the the math major as well as the courses offered by our department that a major might use to complete his or her program. In general, the math major is very flexible and has very few firm requirements. THerefore all students are strongly encouraged to speak with an adviser in order to plan and select their courses.
General Description of Math Course Levels
Math courses at UW-Madison are roughly grouped into three tiers:
- Classes below the 300 level are generally calculus and precalculus courses or various types and flavors. Students who are interested in mathematics as a major typically complete the 221-222-234 calculus sequence (or its equivalent). Well prepared freshmen might instead consider the 375-376 honors calculus sequence as an alternative.
- Classes numbered between 300 and 500 are intermediate level courses classes. These courses typically will have some lower level prerequisites (usually Math 234) and will feature how mathematical concepts evolve into deeper theory and/or applications. At this level you will find our linear algebra courses (a major requirement) as well as courses designed specifically for students interested in secondary education. You will also find our Transition to proof courses and Introductory applied math sequence. We strongly suggest that students take courses from at least one of these two areas before moving into the advanced levels.
- Classes numbered above 500 are our advanced courses including the core 500 level courses in analysis, algebra, and topology. It is our opinion that students who feel comfortable should proceed to this level as quickly as possible. In particular, those students interested in graduate study in mathematics should aim to take 4-8 courses at this level, depending on interests.
Progressing Through the Math Major
The math major requires a course in linear algebra as well as several courses at the intermediate and advanced levels. However, most students will begin somewhere within the calculus sequence. As a student near the end of the calculus sequence they should meet with an adviser in order to discuss the major and associated interests. This is a good time to talk about
- What linear algebra course you should take.
- If an introduction to proofs course is a good idea. (It probably is!)
- Are you interested in an Option 2 Major?
- What Advanced courses you should target.
In general we suggest that students complete at least one transition course and/or the applied math sequence before moving into the upper levels. The following picture indicates the "flow" of coursework from calculus to the upper levels: