Madison Math Circle: Difference between revisions

From UW-Math Wiki
Jump to navigation Jump to search
VisualWikitext
No edit summary
 
Line 1: Line 1:
=What is it?=
[[Image:logo.png|right|600px]]
The UW-Madison math department organizes a series of talks aimed at interested middle school and high school students throughout the semester. Our goal is to present fun talks that give students a taste of interesting ideas in math and science. In the past we've had talks about plasma and weather in outer space, the way images are shaded in video games, and how credit card numbers are securely transmitted over the internet.  


For more information about Math Circles see http://www.mathcircles.org/
For the site in Spanish, visit [[Math Circle de Madison]]
=What is a Math Circle?=
The Madison Math Circle is a weekly series of mathematically based activities aimed at interested middle school and high school students. It is an outreach program organized by the UW Math Department.  Our goal is to provide a taste of exciting ideas in math and science. In the past we've had talks about plasma and weather in outer space, video game graphics, and encryption.  In the sessions, students (and parents) are often asked to explore problems on their own, with the presenter facilitating a discussion. The talks are independent of one another, so new students are welcome at any point.


After each talk we'll have '''pizza''' provided by the Mathematics Department, and students will have an opportunity to mingle and chat with the speaker and with other participants, to ask questions about some of the topics that have been discussed, and also about college, careers in science, etc.
The level of the audience varies quite widely, including a mix of middle school and high school students, and the speakers generally address this by considering subjects that will be interesting for a wide range of students.


'''The Madison Math circle was recently featured in Wisconsin State Journal:''' http://host.madison.com/wsj/news/local/education/local_schools/school-spotlight-madison-math-circle-gives-young-students-a-taste/article_77f5c042-0b3d-11e1-ba5f-001cc4c03286.html
[[Image: MathCircle_2.jpg|550px]] [[Image: MathCircle_4.jpg|550px]]


=Alright, I want to come!=
Great! If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus (and tell us how many people are coming so we can purchase the appropriate amount of pizza!)


If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in Van Vleck Hall room B223, on the UW-Madison campus).  
After each talk we'll have pizza provided by the Mathematics Department, and students will have an opportunity to mingle and chat with the speaker and with other participants, to ask questions about some of the topics that have been discussed, and also about college, careers in science, etc.
'''We'd also appreciate if you click the "Register" link for the date that your group will be attending.'''


'''Parking''' on campus is free at most (but not all) outdoor parking lots after 4:30pm. Parking lots #25 (Elizabeth Waters) and #26 (Observatory Hill) may be the most convenient. These parking lots are on Observatory Drive just west of the intersection with Charter Street. If you park there, then walk east along Observatory Drive to the top of Bascom Hill, then turn right to Van Vleck Hall. See also the map at http://www.map.wisc.edu/?keyword=public%20parking
'''The Madison Math Circle was featured in Wisconsin State Journal:''' [http://host.madison.com/wsj/news/local/education/local_schools/school-spotlight-madison-math-circle-gives-young-students-a-taste/article_77f5c042-0b3d-11e1-ba5f-001cc4c03286.html check it out]!


=Questions?=
=All right, I want to come!=
If you have any questions, suggestions for topics, or so on, just email the '''organizers''' (Ed Dewey, David Dynerman, Nathan Clement, Lalit Jain, Kevin Zamzow, and Philip Matchett Wood): [mailto:math-circle@math.wisc.edu math-circle@math.wisc.edu].


==Talks this semester, Fall 2012==
Our in person talks will be at, <b>Monday at 6pm in 3255 Helen C White Library</b>, during the school year. New students are welcome at any point!  There is no fee and the talks are independent of one another. You can just show up any week, but we ask all participants to take a moment to register by following the link below:
More details about each talk to follow soon. All talks are at '''6pm in Van Vleck Hall, room B223''', unless otherwise noted.


[https://forms.gle/5QRTkHngWf43nmCC9 '''Math Circle Registration Form''']
All of your information is kept private, and is only used by the Madison Math Circle organizer to help run the Circle.
If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus. If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in 3255 Helen C White Library, on the UW-Madison campus, right next to the Memorial Union).
== Fall Schedule ==
<center>
<center>


{| style="color:black; font-size:120%" border="1" cellpadding="14" cellspacing="0"
{| style="color:black; font-size:120%" border="1" cellpadding="14" cellspacing="0"
|-
|-
! Date and RSVP links!! Speaker !! Topic (click for more info) !! Event and poster links
! colspan="4" style="background: #e8b2b2;" align="center" | Fall Schedule
|-
! Date !! Location and Room || Speaker || Title
|-
| Oct 7 || 3255 College Library || Caitlin Davis || How to Cut a Cake (Fairly)
|-
| Oct 14 || 3255 College Library || Uri Andrews || Math, Philosophy, Psychology, and Artificial Intelligence
|-
| Oct 21 || 3255 College Library || Sam Craig || Fractal geometry and the problem of measuring coastlines
|-
| Oct 28 || 3255 College Library || Cancelled || Cancelled
|-
|-
| October 1, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?pli=1&formkey=dFNDTVA0UHdJNXJ4ejlPNHE4WVQ2dlE6MQ#gid=0 Register] || Richard Askey || [[#Counting: to and then beyond the binomial theorem | Counting: to and then beyond the binomial theorem ]] || Combined High School Math Night & Math Circle [http://www.math.wisc.edu/~pmwood/MathCircle/2012-10-01flier.pdf (Poster)]
| Nov 4 || 3255 College Library || Sam Craig || Proofs of the Pythagorean theorem, new and old.
|-
|-
| October 8, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dGRvYm1oUkNOQVBYT1JfZjZ3a1JlWGc6MQ#gid=0 Register] || Philip Matchett Wood || [[#Proofs with Parity | Proofs with Parity]] || Math Circle
| Nov 11 || 3255 College Library || Chenxi Wu || Heron’s method for approximating square roots
|-
|-
| October 15, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dFYtMlJxa2ZkeGNSSmVjVm9jWGlQTEE6MA#gid=0 Register] || Philip Matchett Wood || [[#Fun Flipping Coins | Fun Flipping Coins]] || Math Circle [http://www.math.wisc.edu/~pmwood/MathCircle/2012-10-15.pdf (Poster)]
| Nov 18 || 3255 College Library || Diego Rojas || Non-Transitive Dice: The Math That Doesn’t Play Fair
|-
|-
| October 22, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dFlNTXNMZk9vZ3lPYXQ5LUE1SHNyYVE6MA#gid=0 Register] || Saverio Spagnolie || [[#Random walks: how gamblers lose and microbes diffuse | Random walks: how gamblers lose and microbes diffuse]] || Combined High School Math Night & Math Circle [http://www.math.wisc.edu/~pmwood/MathCircle/2012-10-22flier.pdf (Poster)]
| Nov 25 || 3255 College Library || Kaiyi Huang || A geometric investigation into a space shuttle failure
|-
|-
| October 29, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dDlUWjZvZjFDcV9VeG1DRFpCbER2dEE6MA#gid=0 Register] || Beth Skubak || [[#Non-Euclidean geometry| non-Euclidean geometry]] || Math Circle [http://www.math.wisc.edu/~pmwood/MathCircle/2012-10-29.pdf (Poster)]
| Dec 2 || 3255 College Library || TBA || TBA
|-
| Dec 9 || 3255 College Library || TBA || TBA
|-
| Dec 16 || 3255 College Library || TBA || TBA
|-
|}


</center>
= Fall Abstracts =
=== Abstract 10/7 ===
<center>
{| style="color:black; font-size:100%" table border="2" cellpadding="10" width="700" cellspacing="20"
|-
|-
| November 5, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dDRoQnFkXzItbXZERXhGNjlfbFFIdGc6MA#gid=0 Register] || Mihai Stoiciu || [[#Rubik's Cubes| Rubik's Cubes]] || Combined High School Math Night & Math Circle [http://www.math.wisc.edu/~pmwood/MathCircle/2012-11-05flier.pdf (Poster)]
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Caitlin Davis'''
|-
|-
| November 12, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dC1KV281aGxnVGViMEVtZ19MaVR6R1E6MA#gid=0 Register] || Alison Gordon || [[#Curious Catalan Numbers| Curious Catalan Numbers]] ||
| bgcolor="#BDBDBD"  align="center" | '''Title: How to Cut a Cake (Fairly)'''
|-
|-
| November 19, 2012: [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dDV0ckU4WTVRTnhYUXZuSlExb05SMVE6MA#gid=0 Register] || Gregory Shinault || [[#Tiling Problems| Tiling Problems]] ||
| bgcolor="#BDBDBD"  | 
Imagine you and a friend are sharing a cupcake.  How can you cut the cupcake so that each of you gets your fair share?  If you've ever shared a cupcake (or some other treat) with a friend, you might have an answer! Now what if you're sharing a cake with several friends?  Can we use the same strategy to cut the cake fairly? We'll talk about how math can be used to study questions like this.
|}                                                                       
</center>
 
=== Abstract 10/14 ===
<center>
{| style="color:black; font-size:100%" table border="2" cellpadding="10" width="700" cellspacing="20"
|-
|-
| November 26, 2012:  [https://docs.google.com/a/wisc.edu/spreadsheet/viewform?formkey=dEhnM2MwM095SGpVb1o2YWZMV0xTYXc6MA#gid=0 Register] || Claire Blackman || [[#TBA| TBA]] ||
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Uri Andrews'''
|-
| bgcolor="#BDBDBD" align="center" | '''Title: Math, Philosophy, Psychology, and Artificial Intelligence'''
|-
| bgcolor="#BDBDBD"  | 
People come to understand the truth via a process of arguing. This could be a philosophical debate. This could be an internal dialogue. This could be in a courtroom. This could be deciding with your family where to go for dinner. These are all different forms of argumentation, with different rules for when you are convinced. In a courtroom, you have to be convinced beyond a reasonable doubt, whereas when deciding where to go for dinner, you might just have to look hungriest to win. These processes can be mathematically modeled. Moreover, this is important for the modern goal of teaching a computer how to think and how to understand human reasoning (Artificial Intelligence).
|}                                                                       
</center>
 
 
=== Abstract 10/21 ===
<center>
{| style="color:black; font-size:100%" table border="2" cellpadding="10" width="700" cellspacing="20"
|-
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Sam Craig'''
|-
| bgcolor="#BDBDBD"  align="center" | '''Title: Fractal geometry and the problem of measuring coastlines'''
|-
| bgcolor="#BDBDBD"  | 
A fractal is a shape which looks about the same when you look closely as when you look far away. I will show some examples of fractals that arise in math (like the Sierpinski triangle) and in nature (like the coastline of an island) and discuss the difficulties in determining what the length of a fractal means.
|}                                                                       
</center>
 
=== Abstract 11/4 ===
<center>
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table
|-
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Sam Craig'''
|-
| bgcolor="#BDBDBD" align="center" | '''Title: Proofs of the Pythagorean theorem, new and old.'''
|-
| bgcolor="#BDBDBD" |
The Pythagorean theorem has been known for thousands of years and over that time, people have found a number of different ways to prove the theorem. We will talk about a proof given by Pythagoras, a proof by US President Andrew Garfield, and a very recent proof (that you might have heard of in the news) by Calcea Johnson and Ne'Kiya Jackson.
|}
|}
</center>
=== Abstract 11/11 ===
<center>
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table
|-
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Chenxi Wu'''
|-
| bgcolor="#BDBDBD" align="center" | '''Title:Heron’s method for approximating square roots.'''
|-
| bgcolor="#BDBDBD" |
We will talk about Heron's method for approximating square roots. This will lead us on a journey through approximation methods including Newton's method, through algebraic concepts like the p-adic numbers, and Hensel's Lemma.
|}
</center>
=== Abstract 11/18 ===
<center>
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table
|-
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Diego Rojas'''
|-
| bgcolor="#BDBDBD" align="center" | '''Title:Non-Transitive Dice: The Math That Doesn’t Play Fair.'''
|-
| bgcolor="#BDBDBD" |
What if I told you there’s a set of dice where winning doesn’t follow the rules you expect? In this talk, we’ll explore the strange and surprising world of non-transitive dice, where the usual logic of “if A is better than B, and B is better than C, then A must be better than C” simply falls apart. Using math, probability, and a little imagination, we’ll uncover why these dice defy intuition and how they challenge our understanding of competition and strategy. Get ready to think about games—and math—in a whole new way!
|}
</center>


=== Abstract 11/25 ===
<center>
{| style="color:black; font-size:100%" border="2" cellpadding="10" width="700" cellspacing="20" table
|-
| bgcolor="#e8b2b2" align="center" style="font-size:125%" | '''Kaiyi Huang'''
|-
| bgcolor="#BDBDBD" align="center" | '''Title:A geometric investigation into a space shuttle failure'''
|-
| bgcolor="#BDBDBD" |
We know that a circle has the same width in every direction, but is it the only object that has this property? NASA engineers assumed so, which, together with a string of other mistakes, might have led to the tragic failure of their space shuttle launch. Let’s look further into this problem so that we won’t make the same mistake again!
|}
</center>
</center>


==Directions and parking==


=== Counting: to and then beyond the binomial theorem ===
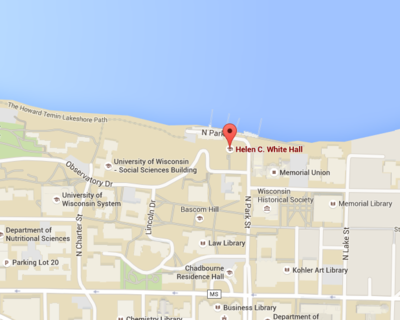
Our meetings are held on the 3rd floor of Helen C. White Hall in room 3255.


<span style="background:#00FF00">October 8th, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
<div class="center" style="width:auto; margin-left:auto; margin-right:auto;">
[[File: Helencwhitemap.png|400px]]</div>


'''Presenter: Richard Askey.''' How many ways can zeros and ones be put into n places?
'''Parking.''' Parking on campus is rather limited.  Here is as list of some options:
It is easy to see this is 2^n.  It is also easy to show that there
are n! ways of ordering n different objects.  There are problems
which go beyond these two.  How many ways can k zeros and n-k ones be
put into n places?  How many inversions are there in the n! ways of
ordering the numbers 1,2,...,n. [123 has no inversions, 132 has one,
312 has two, 321 has three]. These will lead us to what has been
called "The world of q".


*There is a parking garage in the basement of Helen C. White, with an hourly rate.  Enter from Park Street.
*A 0.5 mile walk to Helen C. White Hall via [http://goo.gl/cxTzJY these directions], many spots ('''free starting 4:30pm''') [http://goo.gl/maps/Gkx1C in Lot 26 along Observatory Drive].
*A 0.3 mile walk to Helen C. White Hall via [http://goo.gl/yMJIRd these directions], many spots ('''free starting 4:30pm''') [http://goo.gl/maps/vs17X in Lot 34]. 
*A 0.3 mile walk to Helen C. White Hall via [http://goo.gl/yMJIRd these directions], 2 metered spots (25 minute max) [http://goo.gl/maps/ukTcu in front of Lathrop Hall].
*A 0.2 mile walk to Helen C. White Hall via [http://goo.gl/b8pdk2 these directions] 6 metered spots (25 minute max) around [http://goo.gl/maps/6EAnc the loop in front of Chadbourne Hall] .
*For more information, see the [http://transportation.wisc.edu/parking/parking.aspx UW-Madison Parking Info website].


=== Proofs with Parity ===
==Email list==
The best way to keep up to date with the what is going is by signing up for our email list. Please add your email in the form:
[https://docs.google.com/forms/d/e/1FAIpQLSe_cKMfdjMQlmJc9uZg5bZ-sjKZ2q5SV9wLb1gSddrvB1Tk1A/viewform '''Join Email List''']


<span style="background:#00FF00">October 8th, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
==Contact the organizers==
The Madison Math Circle is organized by a group of professors and graduate students from the [http://www.math.wisc.edu Department of Mathematics] at the UW-Madison. If you have any questions, suggestions for topics, or so on, just email the '''organizers''' [mailto:mathcircleorganizers@g-groups.wisc.edu here]. We are always interested in feedback!
<center>
<gallery widths="500" heights="300" mode="packed">
File:Uri.jpg|[https://www.math.wisc.edu/~andrews/ Prof. Uri Andrews]
</gallery>
 
<gallery widths="500" heights="250" mode="packed">
</gallery>
</center>


'''Presenter: Philip Matchett Wood.''' Parity---matching objects up in pairs---is a surprisingly useful tool for answering math questions.  Bring a pencil and notebook, and we will explore many different situations where parity plays a role.
==Donations==
Please consider donating to the Madison Math Circle. Our main costs consist of pizza and occasional supplies for the speakers.  So far our costs have been covered by donations from the UW Mathematics Department as well as a generous gifts from private donors. The easiest way to donate is to go to the link:


=== Fun Flipping Coins ===
[http://www.math.wisc.edu/donate Online Donation Link]


<span style="background:#00FF00">October 15th, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
There are instructions on that page for donating to the Math Department.  <b> Be sure and add a Gift Note saying that the donation is intended for the "Madison Math Circle"!</b> The money goes into the Mathematics Department Annual Fund and is routed through the University of Wisconsin Foundation, which is convenient for record-keeping, etc.


'''Presenter: Philip Matchett Wood.''' Flip a coin many times, and what happens?  A whole mess of cool probability, that what! Bring a notebook, pencil, and some sharp common sense.   
Alternately, you can bring a check to one of the Math Circle Meetings. If you write a check, be sure to make it payable to the "WFAA" and add the note "Math Circle Donation" on the check.   


Or you can make donations in cash, and we'll give you a receipt.


=== Random walks: how gamblers lose and microbes diffuse ===
==Help us grow!==
If you like Math Circle, please help us continue to grow!  Students, parents, and teachers can help by:
* Like our [https://facebook.com/madisonmathcircle '''Facebook Page'''] and share our events with others!
* Posting our [https://www.math.wisc.edu/wiki/images/Math_Circle_Flyer_2021.pdf '''flyer'''] at schools or anywhere that might have interested students.
* Discussing the Math Circle with students, parents, teachers, administrators, and others.
* Making an announcement about Math Circle at PTO meetings.
* Donating to Math Circle.
Contact the organizers if you have questions or your own ideas about how to help out.


<span style="background:#00FF00">October 22nd, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
=Useful Resources=


'''Presenter: Saverio Spagnolie.''' We will explore one of the most famous mathematical models of random activity, the random walk. After an introduction to some basic ideas from probability, we will see that the same mathematical tools can be used to study completely different types of problems. In particular, we will find that there are no gambling strategies that can be used to beat the casino, and that tiny microorganisms can't stop moving even if they want to!




=== Non-Euclidean geometry ===
== Archived Abstracts ==


<span style="background:#00FF00">October 29th, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2023-2024 2023 - 2024 Abstracts]


'''Presenter: Beth Skubak.'''
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2022-2023 2022 - 2023 Abstracts]
Most of the geometry we see in school is based on the ideas of the Greek mathematician Euclid, who lived around 300 BC. While his ideas are pretty useful, we want to consider geometry in some "non-Euclidean" scenarios, like when instead of being flat, our surfaces are curved.


=== Rubik's Cubes ===
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2021-2022 2021 - 2022 Abstracts]


<span style="background:#00FF00">November 5th, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2020-2021 2020 - 2021 Abstracts]


'''Presenter: Mihai Stoiciu.''' Rubik's Cubes. Some people describe mathematics as the science of patterns. We will explore patterns, permutations, orientations, and counting with the famous Rubik's Cube.
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2019-2020 2019 - 2020 Abstracts]


=== Curious Catalan Numbers ===
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_2016-2017 2016 - 2017 Math Circle Page]


<span style="background:#00FF00">November 12th, 2012, '''6pm''', Van Vleck Hall room B223, UW-Madison campus</span>
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2016-2017 2016 - 2017 Abstracts]


'''Presenter: Alison Gordon.''' Catalan numbers.
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_2015-2016 2015 - 2016 Math Circle Page]


==Talks Next semester, Spring 2013==
[https://www.math.wisc.edu/wiki/index.php/Math_Circle_de_Madison_2015-2016 2015 - 2016 Math Circle Page (Spanish)]
More details about each talk to follow soon. All talks are at '''6pm in Van Vleck Hall, room B223''', unless otherwise noted.


<center>
[https://www.math.wisc.edu/wiki/index.php/Madison_Math_Circle_Abstracts_2015-2016 2015 - 2015 Abstracts]


{| style="color:black; font-size:120%" border="1" cellpadding="14" cellspacing="0"
[https://www.math.wisc.edu/wiki/index.php/Archived_Math_Circle_Material The way-back archives]
|-
! Date !! Speaker !! Talk (click for more info)
|-
| February 4, 2013 || Jonathan Kane || [[#TBA | TBA]]  
|-
| February 1, 2013 || Jean-Luc Thiffeault || [[#TBA | TBA]]
|-
|-
| More TBA ||  ||
|}


</center>
==Link for presenters (in progress)==
[https://www.math.wisc.edu/wiki/index.php/Math_Circle_Presentations  Advice For Math Circle Presenters]


=== TBA ===
[http://www.geometer.org/mathcircles/ Sample Talk Ideas/Problems from Tom Davis]


'''To Be Announced:'''
[https://www.mathcircles.org/activities Sample Talks from the National Association of Math Circles]
Keep an eye out---we'll have more information soon!


==[[Archived Math Circle Material]]==
[https://epdf.pub/circle-in-a-box715623b97664e247f2118ddf7bec4bfa35437.html "Circle in a Box"]
[[Archived Math Circle Material]]

Latest revision as of 15:58, 25 November 2024

Logo.png

For the site in Spanish, visit Math Circle de Madison

What is a Math Circle?

The Madison Math Circle is a weekly series of mathematically based activities aimed at interested middle school and high school students. It is an outreach program organized by the UW Math Department. Our goal is to provide a taste of exciting ideas in math and science. In the past we've had talks about plasma and weather in outer space, video game graphics, and encryption. In the sessions, students (and parents) are often asked to explore problems on their own, with the presenter facilitating a discussion. The talks are independent of one another, so new students are welcome at any point.

The level of the audience varies quite widely, including a mix of middle school and high school students, and the speakers generally address this by considering subjects that will be interesting for a wide range of students.


MathCircle 2.jpg MathCircle 4.jpg


After each talk we'll have pizza provided by the Mathematics Department, and students will have an opportunity to mingle and chat with the speaker and with other participants, to ask questions about some of the topics that have been discussed, and also about college, careers in science, etc.

The Madison Math Circle was featured in Wisconsin State Journal: check it out!

All right, I want to come!

Our in person talks will be at, Monday at 6pm in 3255 Helen C White Library, during the school year. New students are welcome at any point! There is no fee and the talks are independent of one another. You can just show up any week, but we ask all participants to take a moment to register by following the link below: 

Math Circle Registration Form

All of your information is kept private, and is only used by the Madison Math Circle organizer to help run the Circle.

If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus. If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in 3255 Helen C White Library, on the UW-Madison campus, right next to the Memorial Union).


Fall Schedule

Fall Schedule
Date Location and Room Speaker Title
Oct 7 3255 College Library Caitlin Davis How to Cut a Cake (Fairly)
Oct 14 3255 College Library Uri Andrews Math, Philosophy, Psychology, and Artificial Intelligence
Oct 21 3255 College Library Sam Craig Fractal geometry and the problem of measuring coastlines
Oct 28 3255 College Library Cancelled Cancelled
Nov 4 3255 College Library Sam Craig Proofs of the Pythagorean theorem, new and old.
Nov 11 3255 College Library Chenxi Wu Heron’s method for approximating square roots
Nov 18 3255 College Library Diego Rojas Non-Transitive Dice: The Math That Doesn’t Play Fair
Nov 25 3255 College Library Kaiyi Huang A geometric investigation into a space shuttle failure
Dec 2 3255 College Library TBA TBA
Dec 9 3255 College Library TBA TBA
Dec 16 3255 College Library TBA TBA

Fall Abstracts

Abstract 10/7

Caitlin Davis
Title: How to Cut a Cake (Fairly)

Imagine you and a friend are sharing a cupcake. How can you cut the cupcake so that each of you gets your fair share? If you've ever shared a cupcake (or some other treat) with a friend, you might have an answer! Now what if you're sharing a cake with several friends? Can we use the same strategy to cut the cake fairly? We'll talk about how math can be used to study questions like this.

Abstract 10/14

Uri Andrews
Title: Math, Philosophy, Psychology, and Artificial Intelligence

People come to understand the truth via a process of arguing. This could be a philosophical debate. This could be an internal dialogue. This could be in a courtroom. This could be deciding with your family where to go for dinner. These are all different forms of argumentation, with different rules for when you are convinced. In a courtroom, you have to be convinced beyond a reasonable doubt, whereas when deciding where to go for dinner, you might just have to look hungriest to win. These processes can be mathematically modeled. Moreover, this is important for the modern goal of teaching a computer how to think and how to understand human reasoning (Artificial Intelligence).


Abstract 10/21

Sam Craig
Title: Fractal geometry and the problem of measuring coastlines

A fractal is a shape which looks about the same when you look closely as when you look far away. I will show some examples of fractals that arise in math (like the Sierpinski triangle) and in nature (like the coastline of an island) and discuss the difficulties in determining what the length of a fractal means.

Abstract 11/4

Sam Craig
Title: Proofs of the Pythagorean theorem, new and old.

The Pythagorean theorem has been known for thousands of years and over that time, people have found a number of different ways to prove the theorem. We will talk about a proof given by Pythagoras, a proof by US President Andrew Garfield, and a very recent proof (that you might have heard of in the news) by Calcea Johnson and Ne'Kiya Jackson.

Abstract 11/11

Chenxi Wu
Title:Heron’s method for approximating square roots.

We will talk about Heron's method for approximating square roots. This will lead us on a journey through approximation methods including Newton's method, through algebraic concepts like the p-adic numbers, and Hensel's Lemma.

Abstract 11/18

Diego Rojas
Title:Non-Transitive Dice: The Math That Doesn’t Play Fair.

What if I told you there’s a set of dice where winning doesn’t follow the rules you expect? In this talk, we’ll explore the strange and surprising world of non-transitive dice, where the usual logic of “if A is better than B, and B is better than C, then A must be better than C” simply falls apart. Using math, probability, and a little imagination, we’ll uncover why these dice defy intuition and how they challenge our understanding of competition and strategy. Get ready to think about games—and math—in a whole new way!


Abstract 11/25

Kaiyi Huang
Title:A geometric investigation into a space shuttle failure

We know that a circle has the same width in every direction, but is it the only object that has this property? NASA engineers assumed so, which, together with a string of other mistakes, might have led to the tragic failure of their space shuttle launch. Let’s look further into this problem so that we won’t make the same mistake again!

Directions and parking

Our meetings are held on the 3rd floor of Helen C. White Hall in room 3255.

Helencwhitemap.png

Parking. Parking on campus is rather limited. Here is as list of some options:

Email list

The best way to keep up to date with the what is going is by signing up for our email list. Please add your email in the form: Join Email List

Contact the organizers

The Madison Math Circle is organized by a group of professors and graduate students from the Department of Mathematics at the UW-Madison. If you have any questions, suggestions for topics, or so on, just email the organizers here. We are always interested in feedback!

Donations

Please consider donating to the Madison Math Circle. Our main costs consist of pizza and occasional supplies for the speakers. So far our costs have been covered by donations from the UW Mathematics Department as well as a generous gifts from private donors. The easiest way to donate is to go to the link:

Online Donation Link

There are instructions on that page for donating to the Math Department. Be sure and add a Gift Note saying that the donation is intended for the "Madison Math Circle"! The money goes into the Mathematics Department Annual Fund and is routed through the University of Wisconsin Foundation, which is convenient for record-keeping, etc.

Alternately, you can bring a check to one of the Math Circle Meetings. If you write a check, be sure to make it payable to the "WFAA" and add the note "Math Circle Donation" on the check.

Or you can make donations in cash, and we'll give you a receipt.

Help us grow!

If you like Math Circle, please help us continue to grow! Students, parents, and teachers can help by:

  • Like our Facebook Page and share our events with others!
  • Posting our flyer at schools or anywhere that might have interested students.
  • Discussing the Math Circle with students, parents, teachers, administrators, and others.
  • Making an announcement about Math Circle at PTO meetings.
  • Donating to Math Circle.

Contact the organizers if you have questions or your own ideas about how to help out.

Useful Resources

Archived Abstracts

2023 - 2024 Abstracts

2022 - 2023 Abstracts

2021 - 2022 Abstracts

2020 - 2021 Abstracts

2019 - 2020 Abstracts

2016 - 2017 Math Circle Page

2016 - 2017 Abstracts

2015 - 2016 Math Circle Page

2015 - 2016 Math Circle Page (Spanish)

2015 - 2015 Abstracts

The way-back archives

Link for presenters (in progress)

Advice For Math Circle Presenters

Sample Talk Ideas/Problems from Tom Davis

Sample Talks from the National Association of Math Circles

"Circle in a Box"

Retrieved from "https://wiki.math.wisc.edu/index.php?title=Madison_Math_Circle&oldid=27655"