Overview of the undergraduate math program

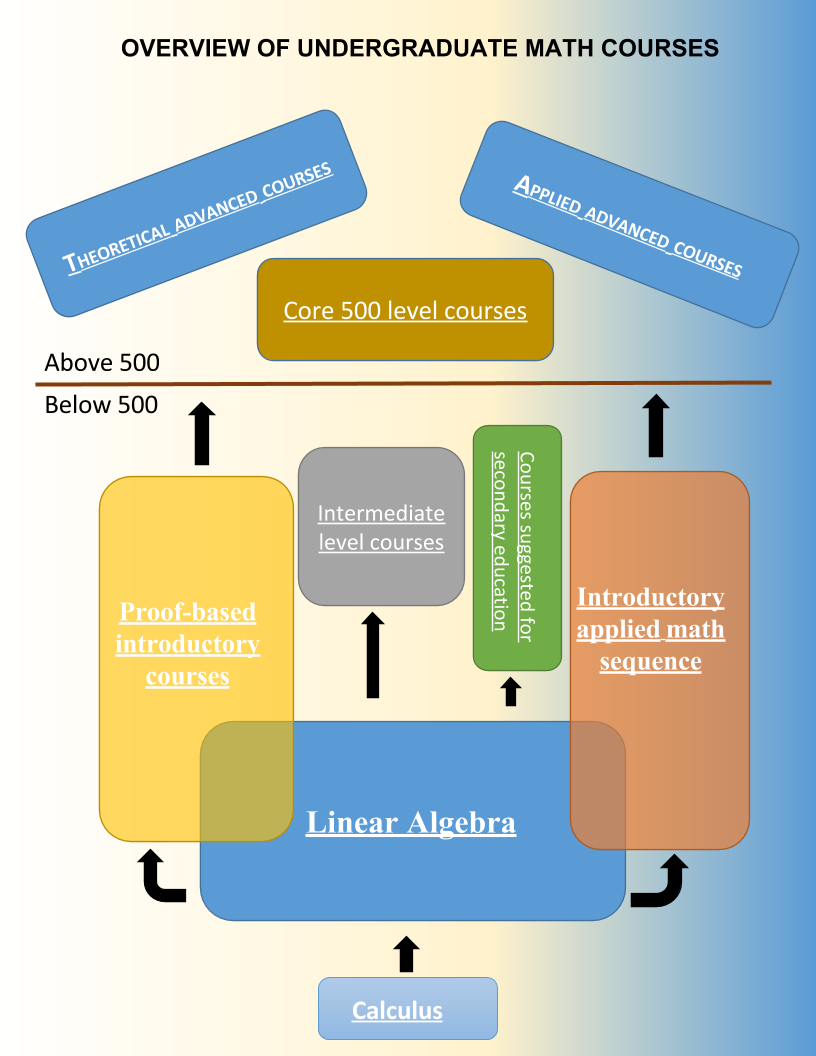
Math courses at UW-Madison are roughly grouped into three tiers:

• Classes below the 300 level are generally calculus and precalculus courses or various types and flavors. Students who are interested in mathematics as a major typically complete the 221-222-234 calculus sequence (or its equivalent). Well prepared students might also consider the 375-376 honors calculus sequence as an alternative.
• Classes numbered between 300 and 500 are intermediate level courses classes. These courses typically will have some lower level prerequisites (usually Math 234) and will feature how mathematical concepts evolve into deeper theory and/or applications. At this level you will find our linear algebra courses (a major requirement) as well as courses designed specifically for students interested in secondary education. You will also find our Transition to proof courses and Introductory applied math sequence. We strongly suggest that students take courses from at least one of these two areas before moving into the advanced levels.
• Classes numbered above 500 are our [[Advanced courses|advanced courses]. It is our opinion that students who feel comfortable should proceed to this level as quickly as possible. In particular, those students interested in graduate study in mathematics should aim to take 4-8 courses at this level, depending on interests. Here is where you will find our core 500 level courses in analysis, algebra, and topology.

To be completed:

Quick Links to Different Types of Math Classes

• Calculus
• Intermediate level courses
• Linear Algebra
• Introductory applied math sequence
• Transition to proof courses
• Courses suggested for secondary education
• Core 500 level courses
• Advanced courses