Madison Math Circle

Weekly Meeting

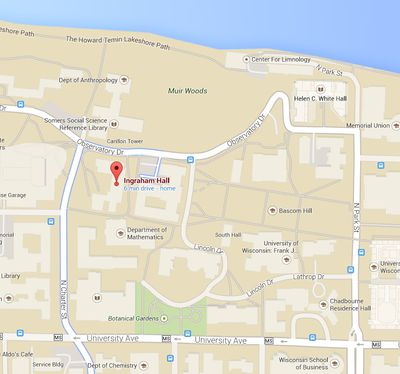
We have a weekly meeting, Monday at 6pm in 120 Ingraham Hall, during the school year. New students are welcome at any point! There is no required registration, no fee, and the talks are independent of one another, so you can just show up any week. See below for directions.

If you are a student, we hope you will tell other interested students about these talks, and speak with your parents or with your teacher about organizing a car pool to the UW campus. If you are a parent or a teacher, we hope you'll tell your students about these talks and organize a car pool to the UW (all talks take place in Ingraham Hall room 120, on the UW-Madison campus).

What is a Math Circle?

The Madison Math Circle is a weekly series of mathematically based activities aimed at interested middle school and high school students. It is an outreach program organized by the UW Math Department. Our goal is to provide a taste of exciting ideas in math and science. In the past we've had talks about plasma and weather in outer space, video game graphics, and encryption. In the sessions, students (and parents) are often asked to explore problems on their own, with the presenter facilitating a discussion. The talks are independent of one another, so new students are welcome at any point.

The level of the audience varies quite widely, including a mix of middle school and high school students, and the speakers generally address this by considering subjects that will be interesting for a wide range of students.

After each talk we'll have pizza provided by the Mathematics Department, and students will have an opportunity to mingle and chat with the speaker and with other participants, to ask questions about some of the topics that have been discussed, and also about college, careers in science, etc.

The Madison Math circle was featured in Wisconsin State Journal: http://host.madison.com/wsj/news/local/education/local_schools/school-spotlight-madison-math-circle-gives-young-students-a-taste/article_77f5c042-0b3d-11e1-ba5f-001cc4c03286.html

All right, I want to come!

Directions and parking

Meetings are held in 120 Ingraham Hall.

Parking. Parking on campus is rather limited. Here is as list of some options:

• Directly in front of Ingraham hall, 2 metered spots (25 minute max) in Lot 11 off of Observatory Drive.
• A 0.2 mile walk to Ingraham Hall via these directions, many spots (free starting 4:30pm) in Lot 26 along Observatory Drive.
• A 0.3 mile walk to Ingraham Hall via these directions, many spots (free starting 4:30pm) in Lot 34.
• A 0.2 mile walk to Ingraham Hall via these directions, 2 metered spots (25 minute max) in front of Lathrop Hall.
• A 0.3 mile walk to Ingraham Hall via these directions 6 metered spots (25 minute max) around the loop in front of Chadbourne Hall .
• For more information, see the UW-Madison Parking Info website.

Email list

Sign up for our email list: https://lists.math.wisc.edu/listinfo/math-circle

Contact the organizers

If you have any questions, suggestions for topics, or so on, just email the organizers (Carolyn Abbott, Gheorghe Craciun, Daniel Erman, Lalit Jain, Ryan Julian, and Philip Matchett Wood): math-circle-organizers@math.wisc.edu. We are always interested in feedback!

Report on Math Circle in 2013-14

Annual Report

Donations!

Please consider donating to the Madison Math Circle. As noted in our annual report, our main costs consist of pizza and occasional supplies for the speakers. Our costs have been covered so far by donations from the UW Math Department plus generous gifts from a private donor. But our costs are rising, primarily because this year we expect to hold more meetings than in any previous year. In fact, this year, we expect to spend at least $2500 on pizza and supplies alone.

So please consider donating to support your math circle! The easiest way to donate is to go to the link:

Donation Link

There are instructions on that page for donating to the Math Department. Be sure and add a Gift Note saying that the donation is intended for the "Madison Math Circle"! The money goes into the Mathematics Department Annual Fund and is routed through the University of Wisconsin Foundation, which is convenient for record-keeping, etc.

Alternately, you can bring a check to one of the Math Circle Meetings. If you write a check, be sure to make it payable to the "University of Wisconsin Math Department" and add the note "Math Circle Donation" on the check.

Flyer

Please feel free to distribute our flyer! Flyer

Help us grow!

If you like Math Circle, please help us continue to grow! Students, parents, and teachers can help by:

• Posting our flyer at schools or anywhere that might have interested students
• Discussing the Math Circle with students, parents, teachers, administrators, and others
• Making an announcement about Math Circle at PTO meetings
• Donating to Math Circle

Contact the organizers if you have questions or your own ideas about how to help out.

Meetings for Fall 2014 and Spring 2015

All talks are at 6pm in Ingraham Hall room 120, unless otherwise noted.

Fall 2014
Date and RSVP links	Speaker	Topic	Link for more info
September 8, 2014	Philip Matchett Wood	Pictures and Puzzles
September 15, 2014	Jen Beichman	Playing with geometric sums
September 22, 2014	DJ Bruce	Is any knot the unknot?
September 29, 2014	Uri Andrews	The games of Criss Cross and Brussels Sprouts
October 6, 2014	David Sondak	Fluids, Math, and Oobleck!
October 13, 2014	George Craciun	Proofs without words (but with plenty of pictures)
October 20, 2014	Scott Hottovy	Coming soon!
October 27, 2014	Daniel Hast	Clock arithmetic and perfect squares: a "Golden Theorem" of reciprocity
November 3, 2014	Alisha Zachariah	Infinity
November 10, 2014	Marko Budisic	Mathematics of epidemics
November 17, 2014	Nigel Boston	Same bad channel
November 24, 2014	Daniel Erman	How to catch a (data) thief Cancelled or weather
December 1, 2014	Daniel Erman	How to catch a (data) thief
Spring 2015
January 26, 2015	TBA	Coming soon!
February 2, 2015	Soledad Benguria	Exploring Palindromes
February 9, 2015	Jeff Linderoth	Coming soon!
February 16, 2015	Simon Marshall	The Ant Walk
February 23, 2015	Uri Andrews	Coming soon!
March 2, 2015	Jordan Ellenberg	Coming soon!
March 9, 2015	Ali Lynch	Mathematical Games and Winning Strategies
March 16, 2015	Daniel Schultheis	Picture Hanging and Secret Algebra
March 23, 2015	Betsy Stovall	Divisibility Cheats
March 30, 2015	No meeting	UW Spring Break
April 6, 2015	Julie Mitchell	Protein Folding and Robot Dances: Understanding the Basics of Kinematic Motion
April 13, 2015	Jessica Lin	Coming soon!
April 20, 2015	DJ Bruce	Coming soon!
April 27, 2015	David Anderson	Coming soon!
May 4, 2015	Daniel Ross	Last meeting of semester!

Abstracts

Philip Matchett Wood

Pictures and Puzzles

When does a simple picture solve a tricky puzzle? Come and learn about how line-and-dot drawing can solve complex puzzles, and create some new puzzles besides!

DJ Bruce

Is any knot the unknot?

Abstract: You're walking home from school, and you pull out your head phones to listen to some tunes. However, inevitably they are a horribly tangled mess, but are they really a knot? We'll talk about what exactly is a knot, and how we can tell when something is not the unknot.

David Sondak

Fluids, Math and Oobleck!

We will explore the magical world of fluids and their relationship to mathematics. As an example of fluids and math in the real world, we will make the living fluid oobleck and discuss some of its mathematical properties.

George Craciun

Proofs without words (but with plenty of pictures)

We will discuss mathematical proofs that can be done using only pictures or figures. If you want to see many such examples you can check out the book "Proofs without Words: Exercises in Visual Thinking" by Roger B. Nelsen. For more information also look at the wikipedia page http://en.wikipedia.org/wiki/Proof_without_words , where you can find links to Java Applets that show animations of proofs without words, such as http://usamts.org/Gallery/G_Gallery.php .

Daniel Hast

Clock arithmetic and perfect squares: a "Golden Theorem" of reciprocity

We'll explore systems of arithmetic where numbers loop back around to zero (like the hours on a clock!), called "modular arithmetic". Which numbers are perfect squares in such systems? Gauss, one of the greatest mathematicians in history, called the remarkable answer the "golden theorem".

Alisha Zachariah

What is infinity anyway

Infinity has a long history of having confounded and fascinated thinkers. We will take a look at some fundamental problems that early mathematicians grappled with and see some ways to understand infinity that have contributed to how we do math today.

Marko Budisic

Mathematics of epidemics

Infectious diseases in our communities often make it into daily conversation: "There's a nasty cold going around.", "It's the flu season, get your shots.", and even, "There are news of a zombie outbreak!" Come hear how math gets applied to something as messy as spread of disease. We will use our wits, pencils, and computers to understand the progress of headaches, common cold, zombie outbreaks, and even ebola, a disease that is currently making the news.

Nigel Boston

Same bad channel

How do we get such clear photos of the comet in the news? A 20 watt transmitter sends signals 500 million km through space to us and yet amazingly they survive this ordeal error-free. What's behind this is error-correcting codes. I'll give some of the basics, some related puzzles, and some challenges.

Soledad Benguria

Exploring Palindromes

A Palindrome is a word or a number that reads the same forward and backwards. For example, Hannah, radar and civic are palindromic words, and 34743, 6446 are palindromic numbers. We will explore some curious properties of palindromes, and talk about what makes the number 196 special.

Simon Marshall

The Ant Walk

An ant is walking on a grid in the plane, but it can only move north or east. How many ways are there for it to get from one square to another? The numbers that appear when we answer this question have a wealth of interesting properties.

Betsy Stovall

Divisibility Cheats

We will discuss simple ways to determine whether one number is evenly divisible by a smaller one and also how to prove these facts. If time permits, we will also look at divisibility rules in bases other than 10.

Julie Mitchell

Protein Folding and Robot Dances: Understanding the Basics of Kinematic Motion

We will learn about motion subject to constraints. Mathematics based on these principles helps us build robots, explains human motion, and helps us model the shape of proteins like enzymes and antibodies.

Archived Math Circle Material

Archived Math Circle Material

Link for presenters (in progress)

https://www.math.wisc.edu/wiki/index.php/Math_Circle_Presentations