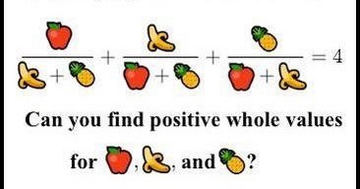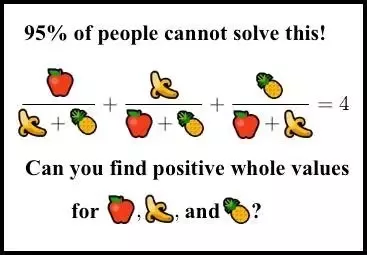AMS Student Chapter Seminar, previous semesters
The AMS Student Chapter Seminar is an informal, graduate student-run seminar on a wide range of mathematical topics.
Past Organizers
Fall 2018 - Spring 2021: Michel Alexis, David Wagner, Patrick Nicodemus, Son Tu, Carrie Chen
Fall 2021 - Spring 2023: Maya Banks, Yandi Wu
Spring 2025
| Date | Speaker | Title | Abstract |
|---|---|---|---|
| January 30 | Caroline Nunn | Watch Caroline eat a donut: an introduction to Morse theory | Morse theory has been described as "one of the deepest applications of differential geometry to topology." However, the concepts involved in Morse theory are so simple that you can learn them just by watching me eat a donut (and subsequently watching me give a 20 minute talk explaining Morse theory.) No background is needed beyond calc 3 and a passing familiarity with donuts. |
| February 6 | Inbo Gottlieb-Fenves | Numbers Modulo One | For millions of years, people have wondered what subsets of the circle are invariant under multiplication by squares. In this talk, I will tell you the answer. |
| February 13 | CANCELLED | NONE | NONE |
| February 20 | Chiara Travesset | The Fold and Cut Theorem | The fold and cut theorem states that any shape consisting of straight sides can be cut from a piece of paper with a single cut by flat folding the paper. Come prepared to do a lot of folding and not a lot of cutting. |
| February 27 | Awildo Gutierrez | Symmetry Arguments in Analysis | Inequalities are hard. But sometimes, you can use symmetries of your objects to upgrade estimates that are much easier to show. Come watch me prove some useful inequalities with this idea. No knowledge of analysis is necessary, just some linear algebra and calculus. |
| March 6 | CANCELLED | NONE | NONE |
| March 13 | Eiki Norizuki | On a theorem of Fermat | A famous theorem of Fermat says that primes that are 1 mod 4 can be written as a sum of two squares. The usual proof that most of us encounter uses some facts about the Gaussian integers Z[i]. I want to talk about an alternative proof that uses windmills. |
| March 19 | Special Visit Day Talks! | See below | See below |
| March 20 | CANCELLED | NONE | NONE |
| March 27 | SPRING BREAK | NONE | NONE |
| April 3 | Emma Hayes | A (Very Brief) Intro to Lean | Lean is an open-source, functional programming language that can be used as an interactive theorem prover. Come watch me attempt to live code to learn the basics of using Lean to prove some fun things. No programming knowledge is necessary. |
| April 10 | Daniel Levitin | A vicious, fire-breathing unlabeled metric space blocks your way. What do you do? | Suppose someone erases the labeling of the real numbers. Can you recover it from just the metric? What about for the Cartesian plane? In this talk I will explain how a clever calculus 1 student could solve this problem, and in so doing, discover the weird world of horospheres. |
| April 17 | Ari Davidovsky | Paley Graphs | A graph G is called k-universal if every possible graph on k vertices is an induced subgraph of G. For many large enough n, most random graphs on n vertices will have this property, but it turns out to be quite difficult to give an explicit construction of a k-universal graph on these n vertices. We will see how to construct a graph that behaves enough like a random graph to be k-universal. |
| April 24 | CANCELLED | NONE | NONE |
| May 1 | Taylor Tan | How to guard a museum | How many guards are needed inside a museum to ensure that every point is secured? Pictures and triangulations — I will challange myself to do this in 1 board. This is a proof from the book (5 lines). |
Visit Day Talks 2025
Visit Day this year is Wednesday, March 19.
| Time | Speaker | Subject | Title and Abstract |
| 10:00-10:30 | Charlotte Moser | Applied/Computational Math | Title: A Stochastic Conceptual Model for the Coupled ENSO and MJO
Abstract: Stochastic ordinary differential equations are simple tools that allow us to model very complex phenomena without the computational expense. Stochastic noise allows us to account for unresolved dynamics that are difficult to model. Here, we model the interactions of the oceanic and atmospheric phenomena El Nino Southern Oscillation (ENSO) and Madden Julian Oscillation (MJO). Since the ocean and the atmosphere are unstable systems, stochastic noise provides a tool to account for the dynamics without numerical blow-up. Such a system is numerically inexpensive and captures accurate statistics that high-dimensional deterministic systems are unable to produce. |
| 10:30-11:00 | Daniel Levitin | Dynamics/Topology/Geometric Group Theory | Title: Life in a Hyperbolic City
Abstract: I will discuss the most important reason prospective students should come to UW Madison: the (almost) locally Euclidean geometry, and how much of a mess it would be to live in a hyperbolic city. I will then talk about some related concepts in geometric group theory. |
| 11:00-11:30 | Bella Finkel | Algebra | Title: A peek at algebraic geometry for scattering amplitudes
Abstract: Combinatorial structures called hypertrees live a double life as on-shell diagrams for N=4 Super Yang Mills theory and objects that parametrize exceptional divisors on the Grothendieck-Knudsen moduli space of stable rational curves. We'll talk about their role as the former, how they give rise to sets of polynomial equations, and what we can do to study the spaces these equations define. |
| 11:30-12:00 | Caroline Nunn | Number Theory | Title: What is a number field, and why?
Abstract: The basic object of study in algebraic number theory is the number field, but why do we care? In this talk, we will explore how problems in elementary number theory lead naturally to the idea of a number field. We will introduce the simplest non-trivial number field, the Gaussian integers, and use their properties to prove cool things, like the classification of Pythagorean triples. No background in number theory is necessary. |
| 12:00-12:30 | Chiara Travesset | Logic | Title: What is Computability Theory?
Abstract: The logic cohort in this department primarily studies Computability Theory—a fascinating field of mathematics that many people have never encountered! Come learn about the study of problems that cannot be solved by any algorithm and how logicians classify them. This classification defines the Turing degrees, which exhibit a remarkably rich structure with many unexpected properties. No prior knowledge of logic is required for this talk. |
| 12:30-2:00 | Lunch | ||
| 2:00-2:30 | Dimas de Albuquerque | Analysis | Title: An Introduction to Fourier Analysis
Abstract: In this talk we’ll discuss the basics of Fourier series, including some of their properties and a quick application to other fields of math. In this route, we’ll pass by some of the most important results in the area, which still guide present day research. |
| 2:30-3:00 | Yahui Qu | Probability | Title: If you like bowling.
Abstract: In the next 30 minutes, I'll introduce our probability group, courses, and seminars. I’ll also briefly talk about my research problems in SPDE and Random Matrix. At the end, I'll answer the question: why the title of this talk is “If you like bowling.” |
| 3:00-3:30 | Adrian Calderon | Partial Differential Equations | Title: An introduction to the level set method and the need for viscosity solutions.
Abstract: In this short talk, I will introduce the level set method and some applications to studying front propagation problems. This method provides a PDE perspective into solving some interesting problems with complicated dynamics. I will then illustrate why we require a weaker notion of solutions to these PDEs and finally define the viscosity solution. |
Fall 2024
Spring 2024
February 1, Sam Craig
Title: A random graph “construction” for k-universal graphs
Abstract: A k-universal graph is a graph G such that any graph H on k vertices is an induced subgraph of G, that is, the vertex set of H is a subset of the vertex set of G and H has the same edges G on those vertices. I will use a random graph model to prove that for sufficiently large values of k, there exists a k-universal graph on k^22^k vertices.
February 8, Ron Yang
Title: Barycentric Subdivision and Random Walks on Groups
Abstract: When applying barycentric subdivisions to a triangle, it is expected that the triangles will become smaller. However, it's nontrivial that they will also become skinnier, i.e., more and more degenerate. We will briefly introduce random walks on groups, specifically on the isometry group of the hyperbolic plane, and explore how Furstenberg's convergence theorem applies.
February 15, Hyun Jong Kim
Title: Not Making an AI Read the Same Piece of Text Over and Over Again Saves Time Maybe?
Abstract: Last year, I talked about trouver, a Python library that I've been developing to use machine learning models to help the user read mathematical text. In this talk, I will talk about one recent update that I've made --- a new model that finds where exactly definitions and notations are introduced in excerpts of mathematical text as opposed to an old model that just finds notations. I will talk about how the two models are different and why the new model is faster.
February 22 Gustavo Flores
Title: Convexity of 4-Maximal Neural Codes
Abstract: A central challenge of neuroscience is deciphering neural code––unpacking the relationship between stimuli and neural activity. Place cells in the hippocampus fire at heightened rates when the organism is in certain regions of its environment, called receptive fields. Experimentally, receptive fields have been shown to have convex shapes. This motivates the question: when do neural codes (as a mathematical object) admit representations via convex shapes in Euclidean space? We (partially) answer this question for 4-maximal codes.
February 29, Jacob Wood
Squitle: Squigonometry
Squabstract: We know that the unit circle x^2+y^2=1 can be parametrized by the sine and cosine functions. How might we be able to parametrize the unit squircle, x^4+y^4=1? We will make new friends, the squigonometric functions, to help us do this. We will compare them to the trig functions by proving some familiar identities and computing properties of this squarametrization.
March 7, CANCELLED
March 14, Hongyu Zhu
Title: Measuring Time with Fuses: What you can and cannot prove
Abstract: You have a candle that burns for a minute. How can you measure half a minute with it? Answer: Light both ends. If you light one end of another candle and light the other end in half a minute, you get 45 seconds. Now if you have an infinite supply of candles (unfortunately not provided), what are all the times that can be measured exactly? These are called the "fusible numbers." In this talk, we will explore what these numbers look like on the real line and, more importantly, when such facts are not provable.
March 20, Visit Day Special Sessions
Speaker: Kaiyi Huang
Title: A generalization of Hölder's inequality and its relation to incidence geometry
Abstract: Given a bunch of lines on a plane, how many joints (where two non-parallel lines intersect) can we have at most? Such elementary problems are studied by mathematicians in areas ranging from algebraic geometry to harmonic analysis. A closely related problem involves a broad class of Lebesgue integral estimates including Hölder's inequality and has broad applications in PDE, statistical mechanics, etc. I am interested in these estimates when “curvature” is introduced.
Speaker: Jiaming Xu
Title: A glimpse of modern probability
Abstract: I will try to provide some flavor about what probabilists are currently studying (it's far beyond random walks and Brownian motions), by giving several examples including random tiling, random matrices, Ising model and stochastic PDEs. These are all important objects in both modern probability, and the work of faculties in our group.
Speaker: Tejasi Bhatnagar
Title: Geometry and arithmetic in characteristic p
Abstract: Going back to 1814, In his famous “last entry”, Gauss recorded the number of rational solutions of some curves over a prime field. His entry was an introduction to a much broader story that led to the development of arithmetic geometry in characteristic p. In this talk, we will walk through some examples and ideas that illustrate the power of unifying geometry and number theory. In particular, we will briefly discuss finding solutions to curves and their Galois theory in characteristic p – where we have a very distinct (but beautiful) intuition from the settings in characteristic 0 that we might be more used to.
Speaker: Allison Byars
Title: Overview of dispersive PDEs
Abstract: In this talk, we’ll go over some typical questions studied in dispersive PDEs. We’ll talk about conservation laws, well-posedness, and long time behavior of solutions all through the model equation of Linear Schr\”odinger. We’ll then see which of these properties still apply in the nonlinear case. Don’t worry if those words don’t mean anything to you, no prior knowledge is necessary!
Speaker: Carsen Grote
Title: Dancing Raisins: levitation and dynamics of bodies in supersaturated fluids
Abstract: A body immersed in a supersaturated fluid like carbonated water can accumulate a dynamic field of bubbles upon its surface. If the body is mobile, the attached bubbles can lift it upward against gravity, but a fluid-air interface can clean the surface of these lifting agents and the body may plummet. The process then begins anew, and continues for as long as the concentration of gas in the fluid supports it. In this work, experiments using fixed and free immersed bodies reveal fundamental features of force development and gas escape. A continuum model which incorporates the dynamics of a surface buoyancy field is used to predict the ranges of body mass and size, and fluid properties, for which the system is most dynamic. Simulations are then used to probe systems which are dominated by a small number of large bubbles.
Speaker: Karthik Ravishankar
Title: Computability theory and its applications
Abstract: In this talk we briefly describe the field of Computability Theory and consider its application to other areas in Mathematics. After a description of the structure of the Turing degrees and a word about how complex this structure is we see how they relate to problems from algebra, analysis and combinatorics.
Speaker: Yandi Wu
Title: Taffy Pullers and Topological Dynamics
Abstract: In this talk, I will explain the mathematics behind taffy pulling machines, which can be modeled by surface homeomorphisms. I will also describe how Thiffeault and Flannagan use “dynamically interesting” surface homeomorphisms (“pseudo-Anosovs”) to build an efficient taffy pulling machine.
Speaker: Caitlyn Davis
Title: A preview of commutative algebra
Abstract: In this talk, we'll discuss some of the objects and questions studied in commutative algebra. We'll discuss the close relationship between algebra and geometry, using the twisted cubic curve as an example. Polynomial rings are some of the central objects of study in commutative algebra, and they have a familiar notion of degree. We'll talk about the surprisingly important role that degree plays in this setting, and about an active area of research that has to do with degree.
March 28, CANCELLED FOR SPRING BREAK
April 4, Chiara Travesset
Title: Linear Temporal Logics
Abstract: Have you ever felt like propositional logic just didn’t have enough operators? Linear temporal logics provide a solution! Come learn about logical operators that allow you to reason over time. We’ll discuss the new operators, some applications, and maybe a third thing.
April 11, Owen Goff
Title: Chromatic Symmetric Functions
Abstract: You may be familiar with symmetric functions -- a type of infinite-variable polynomial that is Schur to please. You may also be familiar with graph colorings. But they are actually intrinsically connected, and the results and patterns can be surprising. In this talk, we will give various definitions and formulas and examples as we seek to connect two vastly different combinatorial theories.
April 18, Sun Woo Park
Title: What I did in my military service III (after working hours)
Abstract: When I was fulfilling military service, I used to play around running codes on Magma after work during evenings. Among the codes I used to run, there is one set of codes which turned out to be very relevant to a research project I focused on during grad school. More specifically, I will try to motivate using examples how understanding the problem of determining whether the number of solutions (x,y) of a given equation from the family {E_n: y^2 = x^3 + 4n^2 x + n^3} ranging over square-free numbers n is infinite or not is closely related to understanding stationary distribution of Markov operators over countable state spaces. (This will be a heavily number-theory flavored talk, but I'll try my best to make the talk as accessible as possible.)
April 25, Alex Mine, the Alpha and the Omega
Title: My Favorite Joke
Abstract: Mathematicians think it's funny to hit small nails with large hammers. I'll tell you about my favorite such joke, about the fundamental group of a topological group. In explaining the joke, I'll hope to convince you that it's not so funny after all.
Fall 2023
September 7, Alex Mine
Title: My Favorite Fact about Continued Fractions
September 14, Mei Rose Connor
Title: All Things Necessary and Possible: an introduction to the Kripke semantics of modal logic
Abstract: Modal logic is a branch of formal logic with far–reaching applications to fields such as philosophy, mathematics, computer science, and other parts of logic itself. It deals with which propositions, some of which are necessarily true (in the words of philosophy, a priori) and some of which are possibly true (analogously, a posteriori). But this will not be a philosophy talk. This talk will cover the notation, syntax, and one choice of semantics for modal logic known as the Kripke semantics. The Kripke semantics is a powerful tool that allows us to make connections between modal statements and first–order (or higher–order) logic ones. Along the way, the talk will explore how the simple symbols □ and ♢ can help to model ethics, represent the knowledge of individuals and even lead to an elegant gateway into the First Incompleteness result.
September 21, Sun Woo Park
Title: What I did in my military service II (A functorial formulation of deep learning algorithms)
Abstract: Even though deep learning algorithms (say convolutional neural networks, graph neural networks, and attention-transformers) show outstanding performances in executing certain tasks, there are also certain tasks that these algorithms do not perform well. We'll try to give a naive attempt to understand why such problems can occur. Similar to last semester, I will once again recall what I was interested in during the last few months of my 3-year military service in South Korea.
September 28, Caroline Nunn
Title: Phinary Numbers
Abstract: Everyone and their grandmother knows about binary numbers. But do you know about phinary numbers? In this talk, we will explore the fun consequences of using an irrational number base system. We will define phinary representations of real numbers and explore which real numbers can be written using finite or recurring phinary representations.
October 5, Gabriella Brown
Title: Topological Entropy in Shift Spaces
Abstract: Entropy is a concept that many STEM disciplines engage with, which results in many different perspectives on what exactly it is. This talk will introduce the perspective of symbolic dynamics by defining shifts of finite type and showing how to compute their topological entropy.
October 12, Nakid Cordero
Title: How to prove the Riemann Hypothesis: a logician's approach
Abstract: Hint: Prove that you cannot disprove it.
October 19, Ari Davidovsky
Title: Using Ultrafilters in Additive Combinatorics
Abstract: The goal of this talk is to introduce the idea of ultrafilters and show how they help us prove some cool results from additive combinatorics. The main result proved will be Hindman's Theorem which states if we partition the natural numbers into finitely many sets then one of these sets A contains an infinite subset B such that the sum of any finitely many distinct elements in B will always be in A.
October 26, Otto Baier
Title: "Circulant Matrices and the Discrete Fourier Transform"
Abstract: "Have you ever tried to use a finite difference method on a differential equation with periodic boundary conditions and said, 'I wonder how I could find the eigenvalues of this matrix analytically'? No? Well either way, you're going to find out!
November 2, CANCELLED
November 9, Owen Goff
Title: Rainbow Permutations
Abstract: Today we will look to see what happens when you generalize the concept of a permutation -- what happens if you can have, say, 2 1s, 2 2s, and 2 3s? Do we still have a group structure? Do we have multiple group structures? How do certain aspects of permutations generalize to these rainbow permutations? Let's find out.
November 16, Sam McKeown
Title:A combinatorial problem in free probability
Abstract: Free probability - as in "probability but free from the onerous assumption that our variables commute with each other". We'll go over the basic definitions and work out an explicit example with a combinatorial interpretation. If time permits, we'll see how this leads into the free central limit theorem.
November 23, CANCELLED FOR THANKSGIVING
November 30, Alex Mine, reprise
Title: An Algebraist's Perspective on the Fourier Transform
Abstract: Alex Mine is an algebraist, and he has a perspective on the Fourier Transform. Sounds neat!
December 7, Maya Banks
Title: A Natural Non-Separated Variety
Abstract: In this last-minute addition, Maya Banks will tell us an example of a natural non-separated variety, and presumably also what all those words mean.
Spring 2023
January 25, Michael Jeserum
Title: Totally Realistic Supply Chains
Abstract: Inspired by a group of fifth and sixth graders, we'll embark on a journey to discover how supply chains definitely work in real life. Along the way, we'll eat donuts, learn about graphs and the magical world of chip-firing, and maybe even make new friends!
February 1, Summer al Hamdani
Title: Monkeying Around: On the Infinite Monkey Theorem
Abstract: Will monkeys keyboard bashing eventually type all of Hamlet? Yes, almost surely. We will discuss the history and proof of the infinite monkey theorem.
February 8, Dionel Jaime
Title: The weird world of polynomial curve fitting.
Abstract: You have some continuous function, and you decide you want to find a polynomial curve that looks a lot like your function. That is a very smart and easy thing to do. Nothing will go wrong.
February 15, Sun Woo Park
Title: What I did in my military service (Universal covers and graph neural networks)
Abstract: I'll try to motivate the relations between universal covers of graphs and graph isomorphism classification tasks implemented from graph neural networks. This is a summary of what I did during my 3 years of leave of absence due to compulsory military service in South Korea. Don't worry, everything I'll present here is already made public and not confidential, so you don't need to worry about the South Korean government officials suddenly appearing during the seminar and accusing me of misconduct!
February 22: NO SEMINAR
February 28, Owen Goff
Title: The RSK Correspondence
Abstract: In this talk I will show a brilliant 1-to-1 mapping between permutations on n elements and pairs of Standard Young Tableau of size n. This bijection, known as the Robinson-Schensted-Knuth correspondence, has many beautiful properties. It also tells you the best way for people to escape a series of rooms.
March 8, Pubo Huang
Title: 2-dimensional Dynamical Billiards
Abstract: We have all played, or watched, a game of pool, and you probably noticed that when a ball hits the cushion on the table, its angle of rebound is equal to its angle of incidence.
Dynamical Billiards is an idealization and generalization of the popular game called pool (or billiards, or snooker), and it aims to understand the trajectory (as time goes to infinity) of a ball on a frictionless table that rebounds perfectly. During the talk, I will provide a lot of examples of dynamical billiards on an actual table and compare it with its mathematical counterpart. We will also see how we can relate billiards on a rectangular table to the classical example of circle rotation in dynamics.
March 15: NO SEMINAR (SPRING BREAK)
March 22: Vicky Wen
Title: On Mostow's Rigidity Theorem
Abstract: Mostow rigidity is one of those famous theorems in hyperbolic geometry that links the topology and geometry of a hyperbolic space (aka a Riemannian manifold with constant curvature -1). It states that in higher dimension (n>2), the geometry of the space is completely determined by its fundamental group, which is a quiet strong and amazing result. In this talk I will try to explain the idea behind the proof and give some counterexamples in dimension 2.
March 24: VISIT DAY SPECIAL SESSIONS
Title: Log concavity properties and combinatorial Hodge theory
Speaker: Colin Crowley
Abstract: Combinatorial Hodge theory is a newly created field (past decade) at the intersection of combinatorics and algebraic geometry. It has lead to proofs of long standing conjectures about matroids, which are objects that generalize finite graphs. I'll introduce some of the main objects, and tell a rough story of how this field came to be.
Title: Commutative algebra and geometry of systems of polynomials
Speaker: Maya Banks
Abstract: When your favorite computer algebra system solves systems of polynomials, it does so by computing something called a Groebner Basis. Groebner bases are collections of polynomials that have many algebraic and geometric properties that make them especially well suited for solving both computational and theoretical problems in commutative algebra and algebraic geometry. I’ll talk about how we (and our computers) make use of these tools and what behind-the-scenes algebra and geometry makes them special.
Title: Markov chains and upper bounds on ranks of quadratic twists of an elliptic curve.
Speaker: Sun Woo Park
Abstract: I will try to give a heuristic argument on how one can use Markov chains to understand the dimensions of some families of finite dimensional vector spaces over F2 (the finite field with 2 elements), which can be used to compute an upper bound on the rank of families of quadratic twists of an elliptic curve. The talk I will deliver will assume background in vector spaces / linear algebra over finite fields, and no prior knowledge about elliptic curves will be required.
Title: Coherent Structures in Convection.
Speaker: Varun Gudibanda
Abstract: Have you ever boiled water? If so, then that's really great I hope you made some tea. It also means that you are familiar with the concept of convection. In convective systems, there are fundamental structures which play an important role in dictating the heat transport and other properties of the system. Let's explore these structures and also learn about how a single number has divided a community of researchers for decades.
Title: Morse Theory in Algebraic Topology (According to ChatGPT)
Speaker: Alex Hof
Title: Life in a Hyperbolic City
Speaker: Daniel Levitin
Abstract: I will discuss the most important reason prospective students should come to UW Madison: the (almost) locally Euclidean geometry, and how much of a mess it would be to live in a hyperbolic city. I will then talk about some related concepts in geometric group theory. This should provide a soft introduction to the colloquium talk as well.
Title: Logic: What is it good for?
Speaker: John Spoerl
Abstract: What are the logicians doing in the math department? Are they philosophers or computer scientists in disguise? (No.) How can I be as cool and mysterious as the logicians? We’ll see how the methods of logic are the most “effective” ways to do mathematics.
Title: Fourier restriction and Kakeya problems
Speaker: Mingfeng Chen
Abstract: Fourier restriction problem was introduced by Elias Stein in the 1970s. It is a central problem in Harmonic analysis. Moreover, restriction problems have close connections with other important questions in Geometric Measure theory(Kakeya problem), Harmonic analysis, combinatorics, number theory and PDE. In this talk, I'm going to give a simple introduction to what it is and what we are going to do.
March 29, Ivan Aidun
Title: Fractional Calculus
Abstract: We teach our calculus students about 1st and 2nd derivatives, but what about 1/2th derivatives? What about πth derivatives? Can we make sense of these derivatives? Can we use them for anything?
April 5, Diego Rojas La Luz
Title: Eating a poisoned chocolate bar
Abstract: Today we are going to talk about Chomp, a game where you take turns eating chocolate and you try not to die from poisoning. This is one of those very easy-to-state combinatoric games which happens to be very hard to fully analyze. We'll see that we can say some surprising things regarding winning strategies, so stay tuned for that. Who wants to play?
April 12, Taylor Tan
Title: A Proof From The Hall of Fame -- Topological Methods in Combinatorics
Abstract: Consider the collection of all n-sets from a 2n+k element ground set. This collection can be partitioned into k+2 partite classes such that there are no intersections between n-sets in the same partite class. In 1955, Kneser conjectured that this bound was sharp, but the problem remained open for two decades until László Lovász gave a proof through topological methods in 1978, thereby inventing the field of topological combinatorics. Another few decades later, a greatly simplified proof (it fits in one paragraph!) was discovered by Joshua Greene and his beautiful proof will be presented in all its glory.
April 19, NO SEMINAR
April 26, Hyun Jong Kim
Title: Machine Learning Tools for the Working Mathematician
Abstract: Mathematicians often have to learn new concepts. I will briefly present trouver, a Python librarythat I have been developing that uses machine learning models to help this process. In particular, trouver can categorize types of mathematical text, identify where notations are introduced in such mathematical text, and attempt to summarize what these notations denote. I will also talk about some high-level ideas go into training such machine learning models in the modern day without huge amounts of data and computational resources.
May 3, Asvin G
Title: On the random graph on countably many vertices
Abstract: I will tell you about "the" graph on countably many vertices. It has many remarkable properties - for instance, any "property" true of it is true for almost all finite graphs!
Spring 2022
February 9, Alex Mine
Title: Would you like to play a game?
Abstract: We'll look at some fun things in combinatorial game theory.
February 16, Michael Jeserum
Title: The Internet's Take on Number Bases
Abstract: Inspired by a TikTok video, we'll embark on a journey to find the best number base to work in*.
*Disclaimer: audience may not actually learn what the best number base is.
February 23, Erika Pirnes
Title: Staying Balanced- studying the balanced algebra
Abstract: The balanced algebra has two generators, R and L, and its defining relations are that any pair of balanced words commutes. For example, RL and LR are balanced (contain the same number of both generators), so in the balanced algebra, (RL)(LR)=(LR)(RL). The goal is to find out which pairs are required to commute in order to make any pair of balanced words commute. This talk includes beautiful mountain landscapes and requires very minimal background knowledge.
March 2, Jason Torchinsky
Title: Holmes and Watson and the case of the tropical climate
Abstract: With a case as complex as the tropical climate, who else could you call? In this talk, we will discuss a strategy for getting models to team up to create a faithful simulation through an analogy of the original sleuthing dynamic duo, Sherlock Holmes and Dr. James Watson.
March 7, Devanshi Merchant
Title: Mathematics of soap films
Abstract: Nature is a miser when it comes to energy. This tendency, in case of soap films motivates mathematicians to study minimal surfaces. This study leads to some beautiful geometry that we will explore.
March 30, Jacob Denson
Title: Proofs in 3 bits or less
Abstract: What can you prove with a string of bits? Is there a proof of Fermat's Last Theorem of the form: "101"? Let's eat donuts, and then talk about it.
April 6, Aidan Howells
Title: Goodstein Sequences, Hercules, and the Hydra
Abstract: We'll discuss Goodstein sequences, Goodstein's theorem, and the Kirby–Paris theorem. We'll relate this to the hydra game of Kirby and Paris. The next time you are supposed to be working, instead check out the hydra game here: http://www.madore.org/~david/math/hydra0.xhtml
Can you beat the hydra? Can you devise a winning strategy, and prove that it always wins? If that's too easy, a harder Hydra game is here: http://www.madore.org/~david/math/hydra.xhtml
April 13, Yu Fu
Title: How do generic properties spread?
Abstract: Given a family of algebraic varieties, a natural question to ask is what type of properties of the generic fiber, and how those properties extend to other fibers. Let's explore this topic from an arithmetic point of view by looking at an example: given a 1-dim family of pairs of elliptic curves with the generic fiber be a pair of isogenous elliptic curves, how the property of 'being isogenous' extend to other fibers?
April 20, Ivan Aidun
Title: The are no Orthogonal Latin Squares of Order 6
Abstract: The title says it all.
Fall 2021
September 29, John Cobb
Title: Rooms on a Sphere
Abstract: A classic combinatorial lemma becomes very simple to state and prove when on the surface of a sphere, leading to easy constructive proofs of some other well known theorems.
October 6, Karan Srivastava
Title: An 'almost impossible' puzzle and group theory
Abstract: You're given a chessboard with a randomly oriented coin on every square and a key hidden under one of them; player one knows where the key is and flips a single coin; player 2, using only the information of the new coin arrangement must determine where the key is. Is there a winning strategy? In this talk, we will explore this classic puzzle in a more generalized context, with n squares and d sided dice on every square. We'll see when the game is solvable and in doing so, see how the answer relies on group theory and the existence of certain groups.
October 13, John Yin
Title: TBA
Abstract: TBA
October 20, Varun Gudibanda
Title: TBA
Abstract: TBA
October 27, Andrew Krenz
Title: The 3-sphere via the Hopf fibration
Abstract: The Hopf fibration is a map from $S^3$ to $S^2$. The preimage (or fiber) of every point under this map is a copy of $S^1$. In this talk I will explain exactly how these circles “fit together” inside the 3-sphere. Along the way we’ll discover some other interesting facts in some hands-on demonstrations using paper and scissors. If there is time I hope to also relate our new understanding of $S^3$ to some other familiar models.
November 3, Asvin G
Title: Probabilistic methods in math
Abstract: I'll explain how you can provr that something has to be true because it's probably true in a couple of examples. One of the proofs is by Erdos on the "sum set problem" and it is a proof that "only an alien could have come up with" according to a friend.
November 10, Ivan Aidun

Title: Intersection Permutations
Abstract: During a boring meeting, your buddy slips you a Paris metro ticket with this cryptic diagram (see right).
What could it mean? The only way to find out is to come to this Donut Talk!
December 1, Yuxi Han
Title: Homocidal Chaffeur Problem
Abstract: I will briefly introduce the canonical example of differential games, called the homicidal chauffeur problem and how to use PDE to run down pedestrians optimally.
December 8, Owen Goff
Title: The Mathematics of Cribbage
Abstract: Cribbage is a card game that I have played many times over the years, that involves, among other things, finding subsets of set of numbers that equal a specific value (in the game that value is 15). In this donut talk I will attempt to use the power of combinatorics to find the optimal strategy for this game, particularly to solve one problem -- is there a way you can guarantee yourself at least one extra point by adding an additional card to your set?
Spring 2020
February 5, Alex Mine
Title: Khinchin's Constant
Abstract: I'll talk about a really weird fact about continued fractions.
February 12, Xiao Shen
Title: Coalescence estimates for the corner growth model with exponential weights
Abstract: (Joint with Timo Seppalainen) I will talk about estimates for the coalescence time of semi-infinite directed geodesics in the planar corner growth model. Not much probability background is needed.
February 19, Hyun Jong Kim
Title: Orbifolds for Music
Abstract: In the first-ever music theory article published by the journal Science, Dmitri Tymoczko uses orbifolds to describe a general framework for thinking about musical tonality. I am going to introduce the musical terms and ideas needed to describe how such orbifolds arise so that we can see an example of Tymoczko's geometric analysis of chord progressions.
February 26, Solly Parenti
Title: Mathematical Measuring
Abstract: What's the best way to measure things? Come find out!
March 4, Cancelled
March 11, Ivan Aidun
Title: The Notorious CRT
Abstract: You're walking up Bascomb hill when a troll suddenly appears and says he'll kill you unless you compute the determinant of
- [math]\displaystyle{ \begin{bmatrix}0 & -7 & -17 & -5 & -13\\8 & -14 & 14 & 11 & 15\\-5 & -17 & 10 & 2 & 10\\17 & 3 & -16 & -13 & 7\\-1 & 2 & -13 & -11 & 10\end{bmatrix} }[/math]
by hand. wdyd?
March 24 - Visit Day (talks cancelled)
Brandon Boggess, Time TBD
Title: TBD
Abstract: TBD
Yandi Wu, Time TBD
Title: TBD
Abstract: TBD
Maya Banks, Time TBD
Title: TBD
Abstract: TBD
Yuxi Han, Time TBD
Title: TBD
Abstract: TBD
Dionel Jaime, Time TBD
Title: TBD
Abstract: TBD
Yun Li, Time TBD
Title: TBD
Abstract: TBD
Erika Pirnes, Time TBD
Title: TBD
Abstract: TBD
Harry Main-Luu, Time TBD
Title: TBD
Abstract: TBD
Kit Newton, Time TBD
Title: TBD
Abstract: TBD
April 1, Ying Li (cancelled)
Title: TBD
Abstract: TBD
April 8, Ben Wright (cancelled)
Title: TBD
Abstract: TBD
April 15, Owen Goff (cancelled)
Title: TBD
Abstract: TBD
Fall 2019
October 9, Brandon Boggess
Title: An Application of Elliptic Curves to the Theory of Internet Memes
Abstract: Solve polynomial equations with this one weird trick! Math teachers hate him!!!
October 16, Jiaxin Jin
Title: Persistence and global stability for biochemical reaction-diffusion systems
Abstract: The investigation of the dynamics of solutions of nonlinear reaction-diffusion PDE systems generated by biochemical networks is a great challenge; in general, even the existence of classical solutions is difficult to establish. On the other hand, these kinds of problems appear very often in biological applications, e.g., when trying to understand the role of spatial inhomogeneities in living cells. We discuss the persistence and global stability properties of special classes of such systems, under additional assumptions such as: low number of species, complex balance or weak reversibility.
October 23, Erika Pirnes
(special edition: carrot seminar)
Title: Why do ice hockey players fall in love with mathematicians? (Behavior of certain number string sequences)
Abstract: Starting with some string of digits 0-9, add the adjacent numbers pairwise to obtain a new string. Whenever the sum is 10 or greater, separate its digits. For example, 26621 would become 81283 and then 931011. Repeating this process with different inputs gives varying behavior. In some cases the process terminates (becomes a single digit), or ends up in a loop, like 999, 1818, 999... The length of the strings can also start growing very fast. I'll discuss some data and conjectures about classifying the behavior.
October 30, Yunbai Cao
Title: Kinetic theory in bounded domains
Abstract: In 1900, David Hilbert outlined 23 important problems in the International Congress of Mathematics. One of them is the Hilbert's sixth problem which asks the mathematical linkage between the mechanics from microscopic view and the macroscopic view. A relative new mesoscopic point of view at that time which is "kinetic theory" was highlighted by Hilbert as the bridge to link the two. In this talk, I will talk about the history and basic elements of kinetic theory and Boltzmann equation, and the role boundary plays for such a system, as well as briefly mention some recent progress.
November 6, Tung Nguyen
Title: Introduction to Chemical Reaction Network
Abstract: Reaction network models are often used to investigate the dynamics of different species from various branches of chemistry, biology and ecology. The study of reaction network has grown significantly and involves a wide range of mathematics and applications. In this talk, I aim to show a big picture of what is happening in reaction network theory. I will first introduce the basic dynamical models for reaction network: the deterministic and stochastic models. Then, I will mention some big questions of interest, and the mathematical tools that are used by people in the field. Finally, I will make connection between reaction network and other branches of mathematics such as PDE, control theory, and random graph theory.
November 13, Jane Davis
Title: Brownian Minions
Abstract: Having lots of small minions help you perform a task is often very effective. For example, if you need to grade a large stack of calculus problems, it is effective to have several TAs grade parts of the pile for you. We'll talk about how we can use random motions as minions to help us perform mathematical tasks. Typically, this mathematical task would be optimization, but we'll reframe a little bit and focus on art and beauty instead. We'll also try to talk about the so-called "storytelling metric," which is relevant here. There will be pictures and animations! 🎉
Sneak preview: some modern art generated with MATLAB.
November 20, Colin Crowley
Title: Matroid Bingo
Abstract: Matroids are combinatorial objects that generalize graphs and matrices. The famous combinatorialist Gian Carlo Rota once said that "anyone who has worked with matroids has come away with the conviction that matroids are one of the richest and most useful ideas of our day." Although his day was in the 60s and 70s, matroids remain an active area of current research with connections to areas such as algebraic geometry, tropical geometry, and parts of computer science. Since this is a doughnut talk, I will introduce matroids in a cute way that involves playing bingo, and then I'll show you some cool examples.
December 4, Xiaocheng Li
Title: The method of stationary phase and Duistermaat-Heckman formula
Abstract: The oscillatory integral $\int_X e^{itf(x)}\mu=:I(t), t\in \mathbb{R}$ is a fundamental object in analysis. In general, $I(t)$ seldom has an explicit expression as Fourier transform is usually inexplicit. In practice, we are interested in the asymptotic behavior of $I(t)$, that is, for $|t|$ very large. A classical tool of getting an approximation is the method of stationary phase which gives the leading term of $I(t)$. Furthermore, there are rare instances for which the approximation coincides with the exact value of $I(t)$. One example is the Duistermaat-Heckman formula in which the Hamiltonian action and the momentum map are addressed. In the talk, I will start with basic facts in Fourier analysis, then discuss the method of stationary phase and the Duistermaat-Heckman formula.
December 11, Chaojie Yuan
Title: Coupling and its application in stochastic chemical reaction network
Abstract: Stochastic models for chemical reaction networks have become increasingly popular in the past few decades. When the molecules are present in low numbers, the chemical system always displays randomness in their dynamics, and the randomness cannot be ignored as it can have a significant effect on the overall properties of the dynamics. In this talk, I will introduce the stochastic models utilized in the context of biological interaction network. Then I will discuss coupling in this context, and illustrate through examples how coupling methods can be utilized for numerical simulations. Specifically, I will introduce two biological models, which attempts to address the behavior of interesting real-world phenomenon.
Spring 2019
February 6, Xiao Shen (in VV B139)
Title: Limit Shape in last passage percolation
Abstract: Imagine the following situation, attached to each point on the integer lattice Z^2 there is an arbitrary amount of donuts. Fix x and y in Z^2, if you get to eat all the donuts along an up-right path between these two points, what would be the maximum amount of donuts you can get? This model is often called last passage percolation, and I will discuss a classical result about its scaling limit: what happens if we zoom out and let the distance between x and y tend to infinity.
February 13, Michel Alexis (in VV B139)
Title: An instructive yet useless theorem about random Fourier Series
Abstract: Consider a Fourier series with random, symmetric, independent coefficients. With what probability is this the Fourier series of a continuous function? An [math]\displaystyle{ L^{p} }[/math] function? A surprising result is the Billard theorem, which says such a series results almost surely from an [math]\displaystyle{ L^{\infty} }[/math] function if and only if it results almost surely from a continuous function. Although the theorem in of itself is kind of useless in of itself, its proof is instructive in that we will see how, via the principle of reduction, one can usually just pretend all symmetric random variables are just coin flips (Bernoulli trials with outcomes [math]\displaystyle{ \pm 1 }[/math]).
February 20, Geoff Bentsen
Title: An Analyst Wanders into a Topology Conference
Abstract: Fourier Restriction is a big open problem in Harmonic Analysis; given a "small" subset [math]\displaystyle{ E }[/math] of [math]\displaystyle{ R^d }[/math], can we restrict the Fourier transform of an [math]\displaystyle{ L^p }[/math] function to [math]\displaystyle{ E }[/math] and retain any information about our original function? This problem has a nice (somewhat) complete solution for smooth manifolds of co-dimension one. I will explore how to start generalizing this result to smooth manifolds of higher co-dimension, and how a topology paper from the 60s about the hairy ball problem came in handy along the way.
February 27, James Hanson
Title: What is...a Topometric Space?
Abstract: Continuous first-order logic is a generalization of first-order logic that is well suited for the study of structures with a natural metric, such as Banach spaces and probability algebras. Topometric spaces are a simple generalization of topological and metric spaces that arise in the study of continuous first-order logic. I will discuss certain topological issues that show up in topometric spaces coming from continuous logic, as well as some partial solutions and open problems. No knowledge of logic will be required for or gained from attending the talk.
March 6, Working Group to establish an Association of Mathematics Graduate Students
Title: Introducing GRAMS (Graduate Representative Association of Mathematics Students)
Abstract: Over the past couple months, a handful of us have been working to create the UW Graduate Representative Association of Mathematics Students (GRAMS). This group, about 5-8 students, is intended to be a liaison between the graduate students and faculty, especially in relation to departmental policies and decisions that affect graduate students. We will discuss what we believe GRAMS ought to look like and the steps needed to implement such a vision, then open up the floor to a Q&A. Check out our website for more information.
March 13, Connor Simpson
Title: Counting faces of polytopes with algebra
Abstract: A natural question is: with a fixed dimension and number of vertices, what is the largest number of d-dimensional faces that a polytope can have? We will outline a proof of the answer to this question.
March 26 (Prospective Student Visit Day), Multiple Speakers
Eva Elduque, 11-11:25
Title: Will it fold flat?
Abstract: Picture the traditional origami paper crane. It is a 3D object, but if you don’t make the wings stick out, it is flat. This is the case for many origami designs, ranging from very simple (like a paper hat), to complicated tessellations. Given a crease pattern on a piece of paper, one might wonder if it is possible to fold along the lines of the pattern and end up with a flat object. We’ll discuss necessary and sufficient conditions for a crease pattern with only one vertex to fold flat, and talk about what can be said about crease patterns with multiple vertices.
Soumya Sankar, 11:30-11:55
Title: An algebro-geometric perspective on integration
Abstract: Integrals are among the most basic tools we learn in complex analysis and yet are extremely versatile. I will discuss one way in which integrals come up in algebraic geometry and the surprising amount of arithmetic and geometric information this gives us.
Chun Gan, 12:00-12:25
Title: Extension theorems in complex analysis
Abstract: Starting from Riemann's extension theorem in one complex variable, there have been many generalizations to different situations in several complex variables. I will talk about Fefferman's field's medal work on Fefferman extension and also the celebrated Ohsawa-Takegoshi L^2 extension theorem which is now a cornerstone for the application of pluripotential theory to complex analytic geometry.
Jenny Yeon, 2:00-2:25
Title: Application of Slope Field
Abstract: Overview of historical problems in Dynamical Systems and what CRN(chemical reaction network) group at UW Madison does. In particular, what exactly is the butterfly effect? Why is this simple-to-state problem so hard even if it is only 2D (Hilbert's 16th problem)? What are some modern techniques availble? What do the members of CRN group do? Is the theory of CRN applicable?
Rajula Srivastava, 2:30-2:55
Title: The World of Wavelets
Abstract: Why the fourier series might not be the best way to represent functions in all cases, and why wavelets might be a good alternative in some of these.
Shengyuan Huang, 3:00-3:25
Title: Group objects in various categories
Abstract: I will introduce categories and talk about group objects in the category of sets and manifolds. The latter leads to the theory of Lie group and Lie algebras. We can then talk about group objects in some other category coming from algebraic geometry and obtain similar results as Lie groups and Lie algebras.
Ivan Ongay Valverde, 3:30-3:55
Title: Games and Topology
Abstract: Studying the topology of the real line leads to really interesting questions and facts. One of them is the relation between some kind of infinite games, called topological games, and specific properties of a subsets of reals. In this talk we will study the perfect set game.
Sun Woo Park, 4:00-4:25
Title: Reconstruction of character tables of Sn
Abstract: We will discuss how we can relate the columns of the character tables of Sn and the tensor product of irreducible representations over Sn. Using the relation, we will also indicate how we can recover some columns of character tables of Sn.
Max Bacharach, 4:30-4:55
Title: Clothes, Lice, and Coalescence
Abstract: A gentle introduction to coalescent theory, motivated by an application which uses lice genetics to estimate when human ancestors first began wearing clothing.
April 3, Yu Feng
Title: Suppression of phase separation by mixing
Abstract: The Cahn-Hilliard equation is a classical PDE that models phase separation of two components. We add an advection term so that the two components are stirred by a velocity. We show that there exists a class of fluid that can prevent phase separation and enforce the solution converges to its average exponentially.
April 17, Hyun Jong Kim
Title: Musical Harmony for the Mathematician
Abstract: Harmony can refer to the way in which multiple notes that are played simultaneously come together in music. I will talk about some aspects of harmony in musical analysis and composition and a few ways to interpret harmonic phenomena mathematically. The mathematical interpretations will mostly revolve around symmetry and integer arithmetic modulo 12.
April 24, Carrie Chen
Title: Pedestrian model
Abstract: When there are lots of people in a supermarket, and for some reason they have to get out as soon as possible, how do you expect the crowd to behave? Suppose each person is a rational individual and assume that each person has all knowledge to other people’s position at every time and further the number of people is huge, we can model it using mean field game model and get the macroscopic behaviour.
Fall 2018
September 26, Vladimir Sotirov
Title: Geometric Algebra
Abstract: Geometric algebra, developed at the end of the 19th century by Grassman, Clifford, and Lipschitz, is the forgotten progenitor of the linear algebra we use to this day developed by Gibbs and Heaviside. In this short introduction, I will use geometric algebra to do two things. First, I will construct the field of complex numbers and the division algebra of the quaternions in a coordinate-free way. Second, I will derive the geometric interpretation of complex numbers and quaternions as representations of rotations in 2- and 3-dimensional space.
October 3, Juliette Bruce
Title: Kissing Conics
Abstract: Have you every wondered how you can easily tell when two plane conics kiss (i.e. are tangent to each other at a point)? If so this talk is for you, if not, well there will be donuts.
October 10, Kurt Ehlert
Title: How to bet when gambling
Abstract: When gambling, typically casinos have the edge. But sometimes we can gain an edge by counting cards or other means. And sometimes we have an edge in the biggest casino of all: the financial markets. When we do have an advantage, then we still need to decide how much to bet. Bet too little, and we leave money on the table. Bet too much, and we risk financial ruin. We will discuss the "Kelly criterion", which is a betting strategy that is optimal in many senses.
October 17, Bryan Oakley
Title: Mixing rates
Abstract: Mixing is a necessary step in many areas from biology and atmospheric sciences to smoothies. Because we are impatient, the goal is usually to improve the rate at which a substance homogenizes. In this talk we define and quantify mixing and rates of mixing. We present some history of the field as well as current research and open questions.
October 24, Micky Soule Steinberg
Title: What does a group look like?
Abstract: In geometric group theory, we often try to understand groups by understanding the metric spaces on which the groups act geometrically. For example, Z^2 acts on R^2 in a nice way, so we can think of the group Z^2 instead as the metric space R^2.
We will try to find (and draw) such a metric space for the solvable Baumslag-Solitar groups BS(1,n). Then we will briefly discuss what this geometric picture tells us about the groups.
October 31, Sun Woo Park
Title: Induction-Restriction Operators
Abstract: Given a "nice enough" finite descending sequence of groups [math]\displaystyle{ G_n \supsetneq G_{n-1} \supsetneq \cdots \supsetneq G_1 \supsetneq \{e\} }[/math], we can play around with the relations between induced and restricted representations. We will construct a formal [math]\displaystyle{ \mathbb{Z} }[/math]-module of induction-restriction operators on a finite descending sequence of groups [math]\displaystyle{ \{G_i\} }[/math], written as [math]\displaystyle{ IR_{\{G_i\}} }[/math]. The goal of the talk is to show that the formal ring [math]\displaystyle{ IR_{\{G_i\}} }[/math] is a commutative polynomial ring over [math]\displaystyle{ \mathbb{Z} }[/math]. We will also compute the formal ring [math]\displaystyle{ IR_{\{S_n\}} }[/math] for a finite descending sequence of symmetric groups [math]\displaystyle{ S_n \supset S_{n-1} \supset \cdots \supset S_1 }[/math]. (Apart from the talk, I'll also prepare some treats in celebration of Halloween.)
November 7, Polly Yu
Title: Positive solutions to polynomial systems using a (mostly linear) algorithm
Abstract: "Wait, did I read the title correctly? Solving non-linear systems using linear methods?” Yes you did. I will present a linear feasibility problem for your favourite polynomial system; if the algorithm returns an answer, you’ve gotten yourself a positive solution to your system, and more than that, the solution set admits a monomial parametrization.
November 14, Soumya Sankar
Title: The worlds of math and dance
Abstract: Are math and dance related? Can we use one to motivate problems in the other? Should we all learn how to dance? I will answer these questions and then we will have some fun with counting problems motivated by dance.
November 28, Niudun Wang
Title: Continued fraction's bizarre adventure
Abstract: When using fractions to approximate a real number, continued fraction is known to be one of the fastest ways. For instance, 3 is close to pi (somehow), 22/7 was the best estimate for centuries, 333/106 is better than 3.1415 and so on. Beyond this, I am going to show how continued fraction can also help us with finding the unit group of some real quadratic fields. In particular, how to solve the notorious Pell's equation.
December 5, Patrick Nicodemus
Title: Applications of Algorithmic Randomness and Complexity
Abstract: I will introduce the fascinating field of Kolmogorov Complexity and point out its applications in such varied areas as combinatorics, statistical inference and mathematical logic. In fact the Prime Number theorem, machine learning and Godel's Incompleteness theorem can all be investigated fruitfully through a wonderful common lens.
December 12, Wanlin Li
Title: Torsors
Abstract: I will talk about the notion of torsor based on John Baez's article 'Torsors made easy' and I will give a lot of examples. This will be a short and light talk to end the semester.
Spring 2017
January 25, Brandon Alberts
Title: Ultraproducts - they aren't just for logicians
Abstract: If any of you have attended a logic talk (or one of Ivan's donut seminar talks) you may have learned about ultraproducts as a weird way to mash sets together to get bigger sets in a nice way. Something particularly useful to set theorists, but maybe not so obviously useful to the rest of us. I will give an accessible introduction to ultraproducts and motivate their use in other areas of mathematics.
February 1, Megan Maguire
Title: Hyperbolic crochet workshop
Abstract: TBA
February 8, Cullen McDonald
February 15, Paul Tveite
Title: Fun with Hamel Bases!
Abstract: If we view the real numbers as a vector field over the rationals, then of course they have a basis (assuming the AOC). This is called a Hamel basis and allows us to do some cool things. Among other things, we will define two periodic functions that sum to the identity function.
February 22, Wil Cocke
Title: Practical Graph Isomorphism
Abstract: Some graphs are different and some graphs are the same. Sometimes graphs differ only in name. When you give me a graph, you've picked an order. But, is it the same graph across every border?
March 1, Megan Maguire
Title: I stole this talk from Jordan.
Abstract: Stability is cool! And sometimes things we think don't have stability secretly do. This is an abridged version of a very cool talk I've seen Jordan give a couple times. All credit goes to him. Man, I should have stolen his abstract too.
March 7, Liban Mohamed
Title: Strichartz Estimates from Qualitative to Quantitative
Abstract: Strichartz estimates are inequalities that give one way understand the decay of solutions to dispersive PDEs. This talk is an attempt to reconcile the formal statements with physical intuition.
March 15, Zachary Charles
Title: Netflix Problem and Chill
Abstract: How are machine learning, matrix analysis, and Napoleon Dynamite related? Come find out!
April 5, Vlad Matei
April 12, Micky Steinberg
Title: Groups as metric spaces
Abstract: Given a group as a set of generators and relations, we can define the “word metric” on the group as the length of the shortest word “between” two elements. This isn’t well-defined, since different generating sets give different metrics, but it is well-defined up to “quasi-isometry”. Come find out what we can do with this! There will lots of pictures and hand-waving!
April 19, Solly Parenti
Title: Elementary Integration
Abstract: Are you like me? Have you also told your calculus students that finding the antiderivative of e^(-x^2) is impossible? Do you also only have a slight idea about how to prove it? Come find out more about the proof and free yourself of that guilt.
April 26, Ben Bruce
Title: Permutation models
Abstract: Permutation models belong to a version of axiomatic set theory known as "set theory with atoms." I will give some examples of permutation models and highlight their connection to the axiom of choice and notions of infinity. There will be concrete examples, and no prior knowledge of set theory is required.
May 3, Iván Ongay-Valverde
Title: Living with countably many reals?
Abstract: Can I make you believe that a countable set of reals are all the reals? If we just have countably many reals, what happens with the others? Do they have any special properties? Let's play a little with our notion of 'reality' and allow to ourselves to find crazy reals doing weird things. Hopefully, no-one's headache will last forever.
Fall 2016
October 12, Soumya Sankar
Title: Primes of certain forms and covering systems
Abstract: A lot of classical questions revolve around primes of the form 2^n + k, where k is an odd integer. I will talk about such primes, or the lack thereof, and use this to convert coffee into covering systems. Time permitting, I'll talk about a few cool results and conjectures related to the notion of covering systems.
October 19, Daniel Hast
Title: A combinatorial lemma in linear algebra
Abstract: I'll talk about a fun little lemma in linear algebra and its combinatorial interpretation. (It might be "well-known" to someone, but I'd never heard of it before.) If there's time, I'll discuss some possible generalizations.
October 26, Brandon Alberts
Title: An Introduction to Matroids
Abstract: What if you wanted to do linear algebra, but couldn't use addition or scalar multiplication? Can we still have a notion of independence and bases? The answer is yes, and these are called matroids. Not only will I introduce matroids, but I will give an example that shows not all matroids arise from vector spaces.
November 2, Vlad Matei
Title: Hadamard Matrices
Abstract: A Hadamard matrix is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal. The most important open question in the theory of Hadamard matrices is that of existence. The Hadamard conjecture proposes that a Hadamard matrix of order 4k exists for every positive integer k. The Hadamard conjecture has also been attributed to Paley, although it was considered implicitly by others prior to Paley's work.
November 9, Juliette Bruce
Title: Some Numbers Are Sometimes Bigger Than Others (Sometimes...)
Abstract: I will write down two numbers and show that one of them is larger than the other.
November 16, Solly Parenti
Title: The Congruent Number Problem
Abstract: To add to the over-romanticization of number theory, I will talk about a simple to state problem about triangles that quickly leads into very difficult open problems in modern number theory.
November 30, Iván Ongay Valverde
Title: Games for fun, games to change the world, games, games, games
Abstract: We will talk about infinite perfect information games. We will discuss different uses for these games, and we will see that some of them have interesting information for us that helps determine some properties of subsets of reals. Can games change the world? Can we use them in a non-intrusive way? Join to have fun with games, since they are games!
December 7, Will Mitchell
Title: An unsolved isomorphism problem from plane geometry
Abstract: A geometric n-configuration is a collection of points and lines in the Euclidean plane such that each point lies on exactly n lines and each line passes through n points. While the study of 3-configurations dates to the nineteenth century, the first example of a 4-configuration appeared only in 1990. I will say a few things about 4-configurations and state an unsolved problem, and I hope that someone in the audience will decide to work on it. There will be nice pictures and a shout-out to the singular value decomposition.
December 14, Paul Tveite
Title: Infinite Chess - Mate in Infinity
Abstract: There's a long history of stating puzzles using chess boards and chess pieces. Particularly endgame puzzles, like so-called "mate in n" problems. When we extend these questions to chess on an infinite board, we get some surprisingly mathematically deep answers.
Spring 2016
January 27, Wanlin Li
Title: The Nottingham group
Abstract: It's the group of wild automorphisms of the local field F_q((t)). It's a finitely generated pro-p group. It's hereditarily just infinite. Every finite p-group can be embedded in it. It's a favorite test case for conjectures concerning pro-p groups. It's the Nottingham group! I will introduce you to this nice pro-p group which is loved by group theorists and number theorists.
February 3, Will Cocke
Title: Who or What is the First Order & Why Should I Care?
Abstract: As noted in recent films, the First Order is very powerful. We will discuss automated theorem proving software, including what exactly that means. We will then demonstrate some theorems, including previously unknown results, whose proofs can be mined from your computer.
February 10, Jason Steinberg
Title: Mazur's Swindle
Abstract: If we sum the series 1-1+1-1+1-1+... in two ways, we get the nonsensical result 0=1 as follows: 0=(1-1)+(1-1)+(1-1)+...=1+(-1+1)+(-1+1)+...=1. While the argument is invalid in the context of adding infinitely many numbers together, there are other contexts throughout mathematics when it makes sense to take arbitrary infinite "sums" of objects in a way that these sums satisfy an infinite form of associativity. In such contexts, the above argument is valid. Examples of such contexts are connected sums of manifolds, disjoint unions of sets, and direct sums of modules, and in each case we can use this kind of argument to achieve nontrivial results fairly easily. Almost too easily...
February 17, Zachary Charles
Title: #P and Me: A tale of permanent complexity
Abstract: The permanent is the neglected younger sibling of the determinant. We will discuss the permanent, its properties, and its applications in graph theory and commutative algebra. We will then talk about computational complexity classes and why the permanent lies at a very strange place in the complexity hierarchy. If time permits, we will discuss operations with even sillier names, such as the immanant.
February 24, Brandon Alberts
Title: The Rado Graph
Abstract: A graph so unique, that a countably infinite random graph is isomorphic to the Rado Graph with probability 1. This talk will define the Rado Graph and walk through a proof of this surprising property.
March 2, Vlad Matei
Title: Pythagoras numbers of fields
Abstract: The Pythagoras number of a field describes the structure of the set of squares in the field. The Pythagoras number p(K) of a field K is the smallest positive integer p such that every sum of squares in K is a sum of p squares.
A pythagorean field is one with Pythagoras number 1: that is, every sum of squares is already a square.
These fields have been studied for over a century and it all started with David Hilbert and his famous 17th problem and whether or not positive polynomial function on R^n can be written as a finite sum of squares of polynomial functions.
We explore the history and various results and some unanswered questions.
March 9, Micky Steinberg
Title: The Parallel Postulate and Non-Euclidean Geometry.
Abstract: “Is Euclidean Geometry true? It has no meaning. We might as well ask if the metric system is true and if the old weights and measures are false; if Cartesian coordinates are true and polar coordinates false. One geometry cannot be more true than another: it can only be more convenient.” -Poincaré
Euclid’s Fifth Postulate is logically equivalent to the statement that there exists a unique line through a given point which is parallel to a given line. For 2000 years, mathematicians were sure that this was in fact a theorem which followed from his first four axioms. In attempts to prove the postulate by contradiction, three mathematicians accidentally invented a new geometry...
March 16, Keith Rush
Title: Fourier series, random series and Brownian motion--the beginnings of modern analysis and probability
Abstract: A mostly historical and (trust me!) non-technical talk on the development of analysis and probability through the interplay between a few fundamental, well-known objects: namely Fourier, random and Taylor series, and the Brownian Motion. In my opinion this is a beautiful and interesting perspective that deserves to be better known. DISCLAIMER: I'll need to end at least 5 minutes early because I'm giving the grad analysis talk at 4.
March 30, Iván Ongay Valverde
Title: Monstrosities out of measure
Abstract: It is a well known result that, using the Lebesgue measure, not all subsets of the real line are measurable. To get this result we use the property of invariance under translation and the axiom of choice. Is this still the case if we remove the invariance over translation? Depending how we answer this question the properties of the universe itself can change.
April 6, Nathan Clement
Title: Algebraic Doughnuts
Abstract: A fun, elementary problem with a snappy solution from Algebraic Geometry. The only prerequisite for this talk is a basic knowledge of circles!
April 13, Adam Frees
Title: The proof is in the 'puting: the mathematics of quantum computing
Abstract: First proposed in the 1980s, quantum computing has since been shown to have a wide variety of practical applications, from finding molecular energies to breaking encryption schemes. In this talk, I will give an introduction to quantum mechanics, describe the basic building blocks of a quantum computer, and (time permitting) demonstrate a quantum algorithm. No prior physics knowledge required!
April 20, Eva Elduque
Title: The Cayley-Hamilton Theorem
Abstract: The Cayley-Hamilton Theorem states that every square matrix with entries in a commutative ring is a root of its characteristic polynomial. We all have used this theorem many times but might have never seen a proof of it. In this talk I will give a slick proof of this result that uses density and continuity so as to prevent the non-algebraists in the room from rioting.
April 27, Juliette Bruce
Title: A Crazy Way to Define Homology
Abstract: This talk will be like a costume party!! However, instead of pretending to be an astronaut I will pretend to be a topologist, and try and say something about the Dold-Thom theorem, which gives a connected between the homotopy groups and homology groups of connected CW complexes. So I guess this talk will be nothing like a costume party, but feel free to wear a costume if you want.
May 4, Paul Tveite
Title: Kissing Numbers (not the fun kind)
Abstract: In sphere packing, the n-dimensional kissing number is the maximal number of non-intersecting radius 1 n-spheres that can all simultaneously be tangent to a central, radius 1 n-sphere. We'll talk a little bit about the known solutions and some of the interesting properties that this problem has.
May 11, Becky Eastham
Title: Logic is Useful for Things, Such as Ramsey Theory
Abstract: Hindman’s Theorem, first proven in 1974, states that every finite coloring of the positive integers contains a monochromatic IP set (a set of positive integers which contains all finite sums of distinct elements of some infinite set). The original proof was long, complicated, and combinatorial. However, there’s a much simpler proof of the theorem using ultrafilters. I’ll tell you what an ultrafilter is, and then I will, in just half an hour, prove Hindman’s Theorem by showing the existence of an idempotent ultrafilter.
Fall 2015
October 7, Eric Ramos
Title: Configuration Spaces of Graphs
Abstract: A configuration of n points on a graph is just a choice of n distinct points. The set of all such configurations is a topological space, and so one can study its properties. Unsurprisingly, one can determine a lot of information about this configuration space from combinatorial data of the graph. In this talk, we consider some of the most basic properties of these spaces, and discuss how they can be applied to things like robotics. Note that most of the talk will amount to drawing pictures until everyone agrees a statement is true.
October 14, Moisés Herradón
Title: The natural numbers form a field
Abstract: But of course, you already knew that they form a field: you just have to biject them into Q and then use the sum and product from the rational numbers. However, out of the many field structures the natural numbers can have, the one I’ll talk about is for sure the cutest. I will discuss how this field shows up in "nature" (i.e. in the games of some fellows of infinite jest) and what cute properties it has.
October 21, Juliette Bruce
Title: Coverings, Dynamics, and Kneading Sequences
Abstract: Given a continuous map f:X—>X of topological spaces and a point x in X one can consider the set {x, f(x), f(f(x)), f(f(f(x))),…} i.e, the orbit of x under the map f. The study of such things even in simple cases, for example when X is the complex numbers and f is a (quadratic) polynomial, turns out to be quite complex (pun sort of intended). (It also gives rise to main source of pretty pictures mathematicians put on posters.) In this talk I want to show how the study of such orbits is related to the following question: How can one tell if a (ramified) covering of S^2 comes from a rational function? No background will be assumed and there will be pretty pictures to stare at.
October 28, Paul Tveite
Title: Gödel Incompleteness, Goodstein's Theorem, and the Hydra Game
Abstract: Gödel incompleteness states, roughly, that there are statements about the natural numbers that are true, but cannot be proved using just Peano Arithmetic. I will give a couple concrete examples of such statements, and prove them in higher mathematics.
November 4, Wanlin Li
Title: Expander Families, Ramanujan graphs, and Property tau
Abstract: Expander family is an interesting topic in graph theory. I will define it, give non-examples and talk about the ideal kind of it, i.e. Ramanujan graph. Also, I will talk about property tau of a group and how it is related to expander families. To make the talk not full of definitions, here are part of the things I'm not going to define: Graph, regular graph, Bipartite graph, Adjacency matrix of a graph and tea...
November 11, Daniel Hast
Title: Scissor groups of polyhedra and Hilbert's third problem
Abstract: Given two polytopes of equal measure (area, volume, etc.), can the first be cut into finitely many polytopic pieces and reassembled into the second? To investigate this question, we will introduce the notion of a "scissor group" and compute the scissor group of polygons. We will also discuss the polyhedral case and how it relates to Dehn's solution to Hilbert's third problem. If there is time, we may mention some fancier examples of scissor groups.
November 18, James Waddington
Note: This week's talk will be from 3:15 to 3:45 instead of the usual time.
Title: Euler Spoilers
Abstract: Leonhard Euler is often cited as one of the greatest mathematicians of the 18. Century. His solution to the Königsburg Bridge problem is an important result of early topology. Euler also did work in combinatorics and in number theory. Often his methods tended to be computational in nature (he was a computer in the traditional sense) and from these he proposed many conjectures, a few of which turned out to be wrong. Two failed conjectures of Euler will be presented.
December 9, Brandon Alberts
Title: The field with one element
December 16, Micky Soule Steinberg
Title: Intersective polynomials
Spring 2015
January 28, Moisés Herradón
Title: Winning games and taking names
Abstract: So let’s say we’re already amazing at playing one game (any game!) at a time and we now we need to play several games at once, to keep it challenging. We will see that doing this results in us being able to define an addition on the collection of all games, and that it actually turns this collection into a Group. I will talk about some of the wonders that lie within the group. Maybe lions? Maybe a field containing both the real numbers and the ordinals? For sure it has to be one of these two!
February 11, Becky Eastham
Title: A generalization of van der Waerden numbers: (a, b) triples and (a_1, a_2, ..., a_n) (n + 1)-tuples
Abstract: Van der Waerden defined w(k; r) to be the least positive integer such that for every r-coloring of the integers from 1 to w(k; r), there is a monochromatic arithmetic progression of length k. He proved that w(k; r) exists for all positive k, r. I will discuss the case where r = 2. These numbers are notoriously hard to calculate: the first 6 of these are 1, 3, 9, 35, 178, and 1132, but no others are known. I will discuss properties of a generalization of these numbers, (a_1, a_2, ..., a_n) (n + 1)-tuples, which are sets of the form {d, a_1x + d, a_2x + 2d, ..., a_nx + nd}, for d, x positive natural numbers.
February 18, Solly Parenti
Title: Chebyshev's Bias
Abstract: Euclid told us that there are infinitely many primes. Dirichlet answered the question of how primes are distributed among residue classes. This talk addresses the question of "Ya, but really, how are the primes distributed among residue classes?" Chebyshev noted in 1853 that there seems to be more primes congruent to 3 mod 4 than their are primes congruent to 1 mod 4. It turns out, he was right, wrong, and everything in between. No analytic number theory is presumed for this talk, as none is known by the speaker.
February 25, Juliette Bruce
Title: Mean, Median, and Mode - Well Actually Just Median
Abstract: Given a finite set of numbers there are many different ways to measure the center of the set. Three of the more common measures, familiar to any middle school students, are: mean, median, mode. This talk will focus on the concept of the median, and why in many ways it's sweet. In particular, we will explore how we can extend the notion of a median to higher dimensions, and apply it to create more robust statistics. It will be awesome, and there will be donuts.
March 4, Jing Hao
Title: Error Correction Codes
Abstract: In the modern world, many communication channels are subject to noise, and thus errors happen. To help the codes auto-correct themselves, more bits are added to the codes to make them more different from each other and therefore easier to tell apart. The major object we study is linear codes. They have nice algebraic structure embedded, and we can apply well-known algebraic results to construct 'nice' codes. This talk will touch on the basics of coding theory, and introduce some famous codes in the coding world, including several prize problems yet to be solved!
March 10 (Tuesday), Nathan Clement
Note: This week's seminar will be on Tuesday at 3:30 instead of the usual time.
Title: Two Solutions, not too Technical, to a Problem to which the Answer is Two
Abstract: A classical problem in Algebraic Geometry is this: Given four pairwise skew lines, how many other lines intersect all of them. I will present some (two) solutions to this problem. One is more classical and ad hoc and the other introduces the Grassmannian variety/manifold and a little intersection theory.
March 25, Eric Ramos
Title: Braids, Knots and Representations
Abstract: In the 1920's Artin defined the braid group, B_n, in an attempt to understand knots in a more algebraic setting. A braid is a certain arrangement of strings in three-dimensional space. It is a celebrated theorem of Alexander that every knot is obtainable from a braid by identifying the endpoints of each string. Because of this correspondence, the Jones and Alexander polynomials, two of the most important knot invariants, can be described completely using the braid group. In fact, Jones was able to show that knot invariants can often be realized as characters of special representations of the braid group.
The purpose of this talk is to give a very light introduction to braid and knot theory. The majority of the talk will be comprised of drawing pictures, and nothing will be treated rigorously.
April 8, James Waddington
Title: Goodstein's Theorem
Abstract: One of the most important results in the development of mathematics are Gödel's Incompleteness theorems. The first incompleteness theorem shows that no list of axioms one could provide could extend number theory to a complete and consistent theory. The second showed that one such statement was no axiomatization of number theory could be used to prove its own consistency. Needless to say this was not viewed as a very natural independent statement from arithmetic.
Examples of non-metamathematical results that were independent of PA, but true of second order number theory, were not discovered until much later. Within a short time of each three such statements that were more "natural" were discovered. The Paris–Harrington Theorem, which was about a statement in Ramsey theory, the Kirby–Paris theorem, which showed the independence of Goodstein's theorem from Peano Arithmetic and the Kruskal's tree theorem, a statement about finite trees.
In this talk I shall discuss Goodstein's theorem which discusses the end behavior of a certain "Zero player" game about k-nary expansions of numbers. I will also give some elements of the proof of the Kirby–Paris theorem.
April 22, William Cocke
Title: Finite Groups aren't too Square
Abstract: We investigate how many non-p-th powers a group can have for a given prime p. We will show using some elementary group theory, that if np(G) is the number of non-p-th powers in a group G, then G has order bounded by np(G)(np(G)+1). Time permitting we will show this bound is strict and that mentioned results involving more than finite groups.
Fall 2014
September 25, Vladimir Sotirov
Title: The compact open topology: what is it really?
Abstract: The compact-open topology on the space C(X,Y) of continuous functions from X to Y is mysteriously generated by declaring that for each compact subset K of X and each open subset V of Y, the continous functions f: X->Y conducting K inside V constitute an open set. In this talk, I will explain the universal property that uniquely determines the compact-open topology, and sketch a pretty constellation of little-known but elementary facts from domain theory that dispell the mystery of the compact-open topology's definition.
October 8, Juliette Bruce
Title: Hex on the Beach
Abstract: The game of Hex is a two player game played on a hexagonal grid attributed in part to John Nash. (This is the game he is playing in /A Beautiful Mind./) Despite being relatively easy to pick up, and pretty hard to master, this game has surprising connections to some interesting mathematics. This talk will introduce the game of Hex, and then explore some of these connections. *As it is a lot more fun once you've actually played Hex feel free to join me at 3:00pm on the 9th floor to actually play a few games of Hex!*
October 22, Eva Elduque
Title: The fold and one cut problem
Abstract: What shapes can we get by folding flat a piece of paper and making (only) one complete straight cut? The answer is surprising: We can cut out any shape drawn with straight line segments. In the talk, we will discuss the two methods of approaching this problem, focusing on the straight skeleton method, the most intuitive of the two.
November 5, Megan Maguire
Title: Train tracks on surfaces
Abstract: What is a train track, mathematically speaking? Are they interesting? Why are they interesting? Come find out!
November 19, Adrian Tovar-Lopez
Title: Hodgkin and Huxley equations of a single neuron
December 3, Zachary Charles
Title: Addition chains: To exponentiation and beyond
Abstract: An addition chain is a sequence of numbers starting at one, such that every number is the sum of two previous numbers. What is the shortest chain ending at a number n? While this is already difficult, we will talk about how addition chains answer life's difficult questions, including: How do we compute 2^4? What can the Ancient Egyptians teach us about elliptic curve cryptography? What about subtraction?