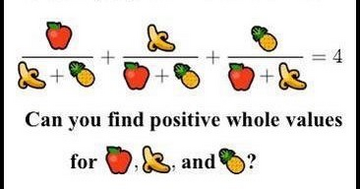AMS Student Chapter Seminar: Difference between revisions
| (247 intermediate revisions by 22 users not shown) | |||
| Line 1: | Line 1: | ||
The AMS Student Chapter Seminar is an informal, graduate student | The AMS Student Chapter Seminar (aka Donut Seminar) is an informal, graduate student seminar on a wide range of mathematical topics. The goal of the seminar is to promote community building and give graduate students an opportunity to communicate fun, accessible math to their peers in a stress-free (but not sugar-free) environment. Pastries (usually donuts) will be provided. | ||
* '''When:''' | * '''When:''' Thursdays 4:00-4:30pm | ||
* '''Where:''' Van Vleck, 9th floor lounge (unless otherwise announced) | * '''Where:''' Van Vleck, 9th floor lounge (unless otherwise announced) | ||
* '''Organizers:''' | * '''Organizers:''' Ivan Aidun, Alex Bonat, Kaiyi Huang, Ethan Schondorf | ||
Everyone is welcome to give a talk. To sign up, please contact one of the organizers with a title and abstract. Talks are | Everyone is welcome to give a talk. To sign up, please contact one of the organizers with a title and abstract. Talks are 25 minutes long and should avoid assuming significant mathematical background beyond first-year graduate courses. | ||
The schedule of talks from past semesters can be found [[AMS Student Chapter Seminar, previous semesters|here]]. | The schedule of talks from past semesters can be found [[AMS Student Chapter Seminar, previous semesters|here]]. | ||
== | == Spring 2025 == | ||
<center> | |||
{| cellspacing="5" cellpadding="14" border="0" style="color:black; font-size:120%" | |||
! align="center" width="200" bgcolor="#D0D0D0" |'''Date''' | |||
! align="center" width="200" bgcolor="#A6B658" |'''Speaker''' | |||
! align="center" width="300" bgcolor="#BCD2EE" |'''Title''' | |||
! align="center" width="400" bgcolor="#BCD2EE" |'''Abstract''' | |||
|- | |||
| bgcolor="#D0D0D0" |January 30 | |||
| bgcolor="#A6B658" |Caroline Nunn | |||
| bgcolor="#BCD2EE" |Watch Caroline eat a donut: an introduction to Morse theory | |||
| bgcolor="#BCD2EE" |Morse theory has been described as "one of the deepest applications of differential geometry to topology." However, the concepts involved in Morse theory are so simple that you can learn them just by watching me eat a donut (and subsequently watching me give a 20 minute talk explaining Morse theory.) No background is needed beyond calc 3 and a passing familiarity with donuts. | |||
|- | |||
| bgcolor="#D0D0D0" |February 6 | |||
| bgcolor="#A6B658" |Inbo Gottlieb-Fenves | |||
| bgcolor="#BCD2EE" |Numbers Modulo One | |||
| bgcolor="#BCD2EE" |For millions of years, people have wondered what subsets of the circle are invariant under multiplication by squares. In this talk, I will tell you the answer. | |||
|- | |||
| bgcolor="#D0D0D0" |February 13 | |||
| bgcolor="#A6B658" |CANCELLED | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
| bgcolor="#D0D0D0" |February 20 | |||
| bgcolor="#A6B658" |Chiara Travesset | |||
| bgcolor="#BCD2EE" |The Fold and Cut Theorem | |||
| bgcolor="#BCD2EE" |The fold and cut theorem states that any shape consisting of straight sides can be cut from a piece of paper with a single cut by flat folding the paper. Come prepared to do a lot of folding and not a lot of cutting. | |||
|- | |||
| bgcolor="#D0D0D0" |February 27 | |||
| bgcolor="#A6B658" |Awildo Gutierrez | |||
| bgcolor="#BCD2EE" |Symmetry Arguments in Analysis | |||
| bgcolor="#BCD2EE" |Inequalities are hard. But sometimes, you can use symmetries of your objects to upgrade estimates that are much easier to show. Come watch me prove some useful inequalities with this idea. No knowledge of analysis is necessary, just some linear algebra and calculus. | |||
|- | |||
| bgcolor="#D0D0D0" |March 6 | |||
| bgcolor="#A6B658" |CANCELLED | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
| bgcolor="#D0D0D0" |March 13 | |||
| bgcolor="#A6B658" |Eiki Norizuki | |||
| bgcolor="#BCD2EE" |On a theorem of Fermat | |||
| bgcolor="#BCD2EE" |A famous theorem of Fermat says that primes that are 1 mod 4 can be written as a sum of two squares. The usual proof that most of us encounter uses some facts about the Gaussian integers Z[i]. I want to talk about an alternative proof that uses windmills. | |||
|- | |||
| bgcolor="#D0D0D0" |March 19 | |||
| bgcolor="#A6B658" |[[AMS Student Chapter Seminar#Visit Day Talks 2025|Special Visit Day Talks!]] | |||
| bgcolor="#BCD2EE" |See below | |||
| bgcolor="#BCD2EE" |See below | |||
|- | |||
| bgcolor="#D0D0D0" | March 20 | |||
| bgcolor="#A6B658" |CANCELLED | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
| bgcolor="#D0D0D0" |March 27 | |||
| bgcolor="#A6B658" |SPRING BREAK | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
| bgcolor="#D0D0D0" | April 3 | |||
| bgcolor="#A6B658" |Emma Hayes | |||
| bgcolor="#BCD2EE" |A (Very Brief) Intro to Lean | |||
| bgcolor="#BCD2EE" |Lean is an open-source, functional programming language that can be used as an interactive theorem prover. Come watch me attempt to live code to learn the basics of using Lean to prove some fun things. No programming knowledge is necessary. | |||
|- | |||
| bgcolor="#D0D0D0" |April 10 | |||
| bgcolor="#A6B658" | Daniel Levitin | |||
| bgcolor="#BCD2EE" |A vicious, fire-breathing unlabeled metric space blocks your way. What do you do? | |||
| bgcolor="#BCD2EE" |Suppose someone erases the labeling of the real numbers. Can you recover it from just the metric? What about for the Cartesian plane? In this talk I will explain how a clever calculus 1 student could solve this problem, and in so doing, discover the weird world of horospheres. | |||
|- | |||
| bgcolor="#D0D0D0" |April 17 | |||
| bgcolor="#A6B658" |TBA | |||
| bgcolor="#BCD2EE" |TBA | |||
| bgcolor="#BCD2EE" |TBA | |||
|- | |||
| bgcolor="#D0D0D0" |April 24 | |||
| bgcolor="#A6B658" |TBA | |||
| bgcolor="#BCD2EE" |TBA | |||
| bgcolor="#BCD2EE" |TBA | |||
|- | |||
| bgcolor="#D0D0D0" |May 1 | |||
| bgcolor="#A6B658" |Ann Bigelow | |||
| bgcolor="#BCD2EE" |TBA | |||
| bgcolor="#BCD2EE" |TBA | |||
|} | |||
</center> | |||
===Visit Day Talks 2025=== | |||
Visit Day this year is Wednesday, March 19. | |||
Title: Geometric Algebra | <center> | ||
{| cellspacing="5" cellpadding="14" border="0" style="color:black; font-size:120%" | |||
|- | |||
| align="center" width="200" bgcolor="#D0D0D0" | '''Time''' | |||
| align="center" width="200" bgcolor="#A6B658" |'''Speaker''' | |||
| align="center" width="300" bgcolor="#BCD2EE" |'''Subject''' | |||
| align="center" width="400" bgcolor="#BCD2EE" |'''Title and Abstract''' | |||
|- | |||
| bgcolor="#E0E0E0" |10:00-10:30 | |||
| bgcolor="#C6D46E" | Charlotte Moser | |||
| bgcolor="#BCE2FE" | Applied/Computational Math | |||
| bgcolor="#BCE2FE" |Title: A Stochastic Conceptual Model for the Coupled ENSO and MJO | |||
Abstract: Stochastic ordinary differential equations are simple tools that allow us to model very complex phenomena without the computational expense. Stochastic noise allows us to account for unresolved dynamics that are difficult to model. Here, we model the interactions of the oceanic and atmospheric phenomena El Nino Southern Oscillation (ENSO) and Madden Julian Oscillation (MJO). Since the ocean and the atmosphere are unstable systems, stochastic noise provides a tool to account for the dynamics without numerical blow-up. Such a system is numerically inexpensive and captures accurate statistics that high-dimensional deterministic systems are unable to produce.<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |10:30-11:00 | |||
| bgcolor="#C6D46E" |Daniel Levitin | |||
| bgcolor="#BCE2FE" |Dynamics/Topology/Geometric Group Theory | |||
| bgcolor="#BCE2FE" |Title: Life in a Hyperbolic City | |||
Abstract: I will discuss the most important reason prospective students should come to UW Madison: the (almost) locally Euclidean geometry, and how much of a mess it would be to live in a hyperbolic city. I will then talk about some related concepts in geometric group theory.<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |11:00-11:30 | |||
| bgcolor="#C6D46E" |Bella Finkel | |||
| bgcolor="#BCE2FE" | Algebra | |||
| bgcolor="#BCE2FE" |Title: A peek at algebraic geometry for scattering amplitudes | |||
Abstract: Combinatorial structures called hypertrees live a double life as on-shell diagrams for N=4 Super Yang Mills theory and objects that parametrize exceptional divisors on the Grothendieck-Knudsen moduli space of stable rational curves. We'll talk about their role as the former, how they give rise to sets of polynomial equations, and what we can do to study the spaces these equations define.<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |11:30-12:00 | |||
| bgcolor="#C6D46E" | Caroline Nunn | |||
| bgcolor="#BCE2FE" |Number Theory | |||
| bgcolor="#BCE2FE" | Title: What is a number field, and why? | |||
Abstract: The basic object of study in algebraic number theory is the number field, but why do we care? In this talk, we will explore how problems in elementary number theory lead naturally to the idea of a number field. We will introduce the simplest non-trivial number field, the Gaussian integers, and use their properties to prove cool things, like the classification of Pythagorean triples. No background in number theory is necessary.<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |12:00-12:30 | |||
| bgcolor="#C6D46E" | Chiara Travesset | |||
| bgcolor="#BCE2FE" | Logic | |||
| bgcolor="#BCE2FE" |Title: What is Computability Theory? | |||
Abstract: The logic cohort in this department primarily studies Computability Theory—a fascinating field of mathematics that many people have never encountered! Come learn about the study of problems that cannot be solved by any algorithm and how logicians classify them. This classification defines the Turing degrees, which exhibit a remarkably rich structure with many unexpected properties. No prior knowledge of logic is required for this talk.<!-- content goes here --> | |||
|- | |||
| bgcolor="#fc9c9c" |12:30-2:00 | |||
| bgcolor="#fc9c9c" |Lunch | |||
| bgcolor="#fc9c9c" |<!-- content goes here --> | |||
| bgcolor="#fc9c9c" |<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |2:00-2:30 | |||
| bgcolor="#C6D46E" |Dimas de Albuquerque | |||
| bgcolor="#BCE2FE" |Analysis | |||
| bgcolor="#BCE2FE" | Title: An Introduction to Fourier Analysis | |||
Abstract: In this talk we’ll discuss the basics of Fourier series, including some of their properties and a quick application to other fields of math. In this route, we’ll pass by some of the most important results in the area, which still guide present day research.<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |2:30-3:00 | |||
| bgcolor="#C6D46E" |Yahui Qu | |||
| bgcolor="#BCE2FE" |Probability | |||
| bgcolor="#BCE2FE" |Title: If you like bowling. | |||
Abstract: In the next 30 minutes, I'll introduce our probability group, courses, and seminars. I’ll also briefly talk about my research problems in SPDE and Random Matrix. At the end, I'll answer the question: why the title of this talk is “If you like bowling.”<!-- content goes here --> | |||
|- | |||
| bgcolor="#E0E0E0" |3:00-3:30 | |||
| bgcolor="#C6D46E" |Adrian Calderon | |||
| bgcolor="#BCE2FE" |Partial Differential Equations | |||
| bgcolor="#BCE2FE" |Title: An introduction to the level set method and the need for viscosity solutions. | |||
Abstract: In this short talk, I will introduce the level set method and some applications to studying front propagation problems. This method provides a PDE perspective into solving some interesting problems with complicated dynamics. I will then illustrate why we require a weaker notion of solutions to these PDEs and finally define the viscosity solution.<!-- content goes here --> | |||
|} | |||
Abstract | ==Fall 2024== | ||
<center> | |||
{| cellspacing="5" cellpadding="14" border="0" style="color:black; font-size:120%" | |||
! align="center" width="200" bgcolor="#D0D0D0" |'''Date''' | |||
! align="center" width="200" bgcolor="#A6B658" |'''Speaker''' | |||
! align="center" width="300" bgcolor="#BCD2EE" |'''Title''' | |||
! align="center" width="400" bgcolor="#BCD2EE" |'''Abstract''' | |||
|- | |||
| bgcolor="#D0D0D0" |September 12 | |||
| bgcolor="#A6B658" |Ari Davidovsky | |||
| bgcolor="#BCD2EE" |95% of people can't solve this! | |||
| bgcolor="#BCD2EE" |[[File:Image.png|360px]] | |||
=== | We will attempt to answer this question and along the way explore how algebra and geometry work together to solve problems in number theory. | ||
|- | |||
| bgcolor="#D0D0D0" |September 19 | |||
| bgcolor="#A6B658" | CANCELLED | |||
| bgcolor="#BCD2EE" | NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
| bgcolor="#D0D0D0" |September 26 | |||
| bgcolor="#A6B658" |Mateo Morales | |||
| bgcolor="#BCD2EE" | Officially petitioning the department to acquire a ping pong table. | |||
| bgcolor="#BCD2EE" |Ever want to prove something is a free group of rank 2? Me too. One way to do this is to use a ping pong argument of how a group generated by two elements acts on a set. | |||
I will illustrate the ping pong argument using an example of matrices, explain how it works, and explain why, kinda. | |||
Very approachable if you know what a group is but does require tons of ping pong experience. | |||
|- | |||
| bgcolor="#D0D0D0" |October 3 | |||
| bgcolor="#A6B658" |Karthik Ravishankar | |||
= | | bgcolor="#BCD2EE" |Incompleteness for the working mathematician | ||
| bgcolor="#BCD2EE" |In this talk we'll take a look at Gödels famous incompleteness theorems and look at some of its immediate as well as interesting consequences. No background in logic is necessary! | |||
|- | |||
| bgcolor="#D0D0D0" |October 10 | |||
| bgcolor="#A6B658" |Elizabeth Hankins | |||
| bgcolor="#BCD2EE" | Mathematical Origami and Flat-Foldability | |||
= | | bgcolor="#BCD2EE" |If you've ever unfolded a piece of origami, you might have noticed complicated symmetries in the pattern of creases left behind. What patterns of lines can and cannot be folded into origami? And why is it sometimes hard to determine? | ||
|- | |||
| bgcolor="#D0D0D0" |October 17 | |||
| bgcolor="#A6B658" |CANCELLED | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
= | |- | ||
| bgcolor="#D0D0D0" |October 24 | |||
| bgcolor="#A6B658" |CANCELLED | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
= | | bgcolor="#D0D0D0" |October 31 | ||
| bgcolor="#A6B658" |Jacob Wood | |||
| bgcolor="#BCD2EE" |What is the length of a <s>potato</s> pumpkin? | |||
| bgcolor="#BCD2EE" |How many is a jack-o-lantern? What is the length of a pumpkin? These questions sound like nonsense, but they have perfectly reasonable interpretations with perfectly reasonable answers. On our journey through the haunted house with two rooms, we will encounter some scary characters like differential topology and measure theory. Do not fear; little to no experience in either subject is required. | |||
|- | |||
| bgcolor="#D0D0D0" |November 7 | |||
= | | bgcolor="#A6B658" |CANCELLED: DISTINGUISHED LECTURE | ||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
|- | |||
| bgcolor="#D0D0D0" |November 14 | |||
| bgcolor="#A6B658" |Sapir Ben-Shahar | |||
= | | bgcolor="#BCD2EE" |Hexaflexagons | ||
| bgcolor="#BCD2EE" |Come along for some hexaflexafun and discover the mysterious properties of hexaflexagons, the bestagons! Learn how to make and navigate through the folds of your very own paper hexaflexagon. No prior knowledge of hexagons (or hexaflexagons) is assumed. | |||
|- | |||
| bgcolor="#D0D0D0" |November 21 | |||
| bgcolor="#A6B658" |Andrew Krenz | |||
| bgcolor="#BCD2EE" |All concepts are database queries | |||
= | | bgcolor="#BCD2EE" |A celebrated result of applied category theory states that the category of small categories is equivalent to the category of database schemas. Therefore, every theorem about small categories can be interpreted as a theorem about databases. Maybe you've heard someone repeat Mac Lane's famous slogan "all concepts are Kan extensions." In this talk, I'll give a high-level overview of/introduction to categorical database theory (developed by David Spivak) wherein Kan extensions play the role of regular every day database queries. No familiarity with categories or databases will be assumed. | ||
|- | |||
| bgcolor="#D0D0D0" |November 28 | |||
| bgcolor="#A6B658" |THANKSGIVING | |||
| bgcolor="#BCD2EE" |NONE | |||
| bgcolor="#BCD2EE" |NONE | |||
= | |- | ||
| bgcolor="#D0D0D0" |December 5 | |||
| bgcolor="#A6B658" |Ivan Aidun | |||
| bgcolor="#BCD2EE" |Impromptu talk | |||
| bgcolor="#BCD2EE" |Caroline is sick today, so Ivan will give an impromptu talk about something. | |||
|} | |||
= | </center> | ||
=== | |||
Latest revision as of 16:21, 9 April 2025
The AMS Student Chapter Seminar (aka Donut Seminar) is an informal, graduate student seminar on a wide range of mathematical topics. The goal of the seminar is to promote community building and give graduate students an opportunity to communicate fun, accessible math to their peers in a stress-free (but not sugar-free) environment. Pastries (usually donuts) will be provided.
- When: Thursdays 4:00-4:30pm
- Where: Van Vleck, 9th floor lounge (unless otherwise announced)
- Organizers: Ivan Aidun, Alex Bonat, Kaiyi Huang, Ethan Schondorf
Everyone is welcome to give a talk. To sign up, please contact one of the organizers with a title and abstract. Talks are 25 minutes long and should avoid assuming significant mathematical background beyond first-year graduate courses.
The schedule of talks from past semesters can be found here.
Spring 2025
| Date | Speaker | Title | Abstract |
|---|---|---|---|
| January 30 | Caroline Nunn | Watch Caroline eat a donut: an introduction to Morse theory | Morse theory has been described as "one of the deepest applications of differential geometry to topology." However, the concepts involved in Morse theory are so simple that you can learn them just by watching me eat a donut (and subsequently watching me give a 20 minute talk explaining Morse theory.) No background is needed beyond calc 3 and a passing familiarity with donuts. |
| February 6 | Inbo Gottlieb-Fenves | Numbers Modulo One | For millions of years, people have wondered what subsets of the circle are invariant under multiplication by squares. In this talk, I will tell you the answer. |
| February 13 | CANCELLED | NONE | NONE |
| February 20 | Chiara Travesset | The Fold and Cut Theorem | The fold and cut theorem states that any shape consisting of straight sides can be cut from a piece of paper with a single cut by flat folding the paper. Come prepared to do a lot of folding and not a lot of cutting. |
| February 27 | Awildo Gutierrez | Symmetry Arguments in Analysis | Inequalities are hard. But sometimes, you can use symmetries of your objects to upgrade estimates that are much easier to show. Come watch me prove some useful inequalities with this idea. No knowledge of analysis is necessary, just some linear algebra and calculus. |
| March 6 | CANCELLED | NONE | NONE |
| March 13 | Eiki Norizuki | On a theorem of Fermat | A famous theorem of Fermat says that primes that are 1 mod 4 can be written as a sum of two squares. The usual proof that most of us encounter uses some facts about the Gaussian integers Z[i]. I want to talk about an alternative proof that uses windmills. |
| March 19 | Special Visit Day Talks! | See below | See below |
| March 20 | CANCELLED | NONE | NONE |
| March 27 | SPRING BREAK | NONE | NONE |
| April 3 | Emma Hayes | A (Very Brief) Intro to Lean | Lean is an open-source, functional programming language that can be used as an interactive theorem prover. Come watch me attempt to live code to learn the basics of using Lean to prove some fun things. No programming knowledge is necessary. |
| April 10 | Daniel Levitin | A vicious, fire-breathing unlabeled metric space blocks your way. What do you do? | Suppose someone erases the labeling of the real numbers. Can you recover it from just the metric? What about for the Cartesian plane? In this talk I will explain how a clever calculus 1 student could solve this problem, and in so doing, discover the weird world of horospheres. |
| April 17 | TBA | TBA | TBA |
| April 24 | TBA | TBA | TBA |
| May 1 | Ann Bigelow | TBA | TBA |
Visit Day Talks 2025
Visit Day this year is Wednesday, March 19.
| Time | Speaker | Subject | Title and Abstract |
| 10:00-10:30 | Charlotte Moser | Applied/Computational Math | Title: A Stochastic Conceptual Model for the Coupled ENSO and MJO
Abstract: Stochastic ordinary differential equations are simple tools that allow us to model very complex phenomena without the computational expense. Stochastic noise allows us to account for unresolved dynamics that are difficult to model. Here, we model the interactions of the oceanic and atmospheric phenomena El Nino Southern Oscillation (ENSO) and Madden Julian Oscillation (MJO). Since the ocean and the atmosphere are unstable systems, stochastic noise provides a tool to account for the dynamics without numerical blow-up. Such a system is numerically inexpensive and captures accurate statistics that high-dimensional deterministic systems are unable to produce. |
| 10:30-11:00 | Daniel Levitin | Dynamics/Topology/Geometric Group Theory | Title: Life in a Hyperbolic City
Abstract: I will discuss the most important reason prospective students should come to UW Madison: the (almost) locally Euclidean geometry, and how much of a mess it would be to live in a hyperbolic city. I will then talk about some related concepts in geometric group theory. |
| 11:00-11:30 | Bella Finkel | Algebra | Title: A peek at algebraic geometry for scattering amplitudes
Abstract: Combinatorial structures called hypertrees live a double life as on-shell diagrams for N=4 Super Yang Mills theory and objects that parametrize exceptional divisors on the Grothendieck-Knudsen moduli space of stable rational curves. We'll talk about their role as the former, how they give rise to sets of polynomial equations, and what we can do to study the spaces these equations define. |
| 11:30-12:00 | Caroline Nunn | Number Theory | Title: What is a number field, and why?
Abstract: The basic object of study in algebraic number theory is the number field, but why do we care? In this talk, we will explore how problems in elementary number theory lead naturally to the idea of a number field. We will introduce the simplest non-trivial number field, the Gaussian integers, and use their properties to prove cool things, like the classification of Pythagorean triples. No background in number theory is necessary. |
| 12:00-12:30 | Chiara Travesset | Logic | Title: What is Computability Theory?
Abstract: The logic cohort in this department primarily studies Computability Theory—a fascinating field of mathematics that many people have never encountered! Come learn about the study of problems that cannot be solved by any algorithm and how logicians classify them. This classification defines the Turing degrees, which exhibit a remarkably rich structure with many unexpected properties. No prior knowledge of logic is required for this talk. |
| 12:30-2:00 | Lunch | ||
| 2:00-2:30 | Dimas de Albuquerque | Analysis | Title: An Introduction to Fourier Analysis
Abstract: In this talk we’ll discuss the basics of Fourier series, including some of their properties and a quick application to other fields of math. In this route, we’ll pass by some of the most important results in the area, which still guide present day research. |
| 2:30-3:00 | Yahui Qu | Probability | Title: If you like bowling.
Abstract: In the next 30 minutes, I'll introduce our probability group, courses, and seminars. I’ll also briefly talk about my research problems in SPDE and Random Matrix. At the end, I'll answer the question: why the title of this talk is “If you like bowling.” |
| 3:00-3:30 | Adrian Calderon | Partial Differential Equations | Title: An introduction to the level set method and the need for viscosity solutions.
Abstract: In this short talk, I will introduce the level set method and some applications to studying front propagation problems. This method provides a PDE perspective into solving some interesting problems with complicated dynamics. I will then illustrate why we require a weaker notion of solutions to these PDEs and finally define the viscosity solution. |